Erwartungswert: Unterschied zwischen den Versionen
Solmyr (Diskussion | Beiträge) (→Blatt 2) |
Solmyr (Diskussion | Beiträge) (Externer-Link zu Solo Tabelle) |
||
| (12 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Quelle:[[Essener System#Stärke der Erstansage|ES 2.1.1]] | Quelle:[[Essener System#Stärke der Erstansage|ES 2.1.1]] | ||
| + | |||
| + | Die Stärke des eigenen Blattes wird am besten ausgedrückt durch eine durchschnittlich damit erreichbare Augenzahl. Die Berechnung dieser Augenzahl erfolgt über die Abschätzung von Erwartungswerten für potentielle Stiche. | ||
| + | |||
| + | Wieviel Augen ist eine Dulle im Durchschnitt wert? Wieviel Augen mache ich normal, wenn ich [[Datei:Kreuz.gif]] oder [[Datei:Pik.gif]] frei bin [[Chicane]]? | ||
| + | |||
| + | Der Erwartungswert ist das Produkt aus dem Wert eines Stiches und der Wahrscheinlichkeit diesen Stich tatsächlich zu erhalten. Erwartungswerte helfen bei der Abschätzung, ob man als erster Re oder kontra ansagen soll/kann/muss. | ||
| + | |||
| + | Die folgende Tabelle zeigt ein einfaches Schema zur Abschätzung dieser Werte. (vgl. [[Mindestblattstärke für eine Erstansage]]) | ||
=Tabelle= | =Tabelle= | ||
| Zeile 25: | Zeile 33: | ||
zweiten Lauf ([[Single|Singleton]]) | zweiten Lauf ([[Single|Singleton]]) | ||
|= eigene Stechkarte + 10 bis 25 | |= eigene Stechkarte + 10 bis 25 | ||
| − | Beachte: Der Wert hängt stark | + | Beachte: Der Wert hängt stark |
| − | + | vom ersten Lauf ab | |
|1/2 (bei Chicane = 2/3) | |1/2 (bei Chicane = 2/3) | ||
Beachte: Die Wahrscheinlichkeit | Beachte: Die Wahrscheinlichkeit | ||
wird durch den ersten | wird durch den ersten | ||
| − | Lauf | + | Lauf beinflusst. |
|- | |- | ||
|3 | |3 | ||
| Zeile 94: | Zeile 102: | ||
Einzelwahrscheinlichkeiten. | Einzelwahrscheinlichkeiten. | ||
|} | |} | ||
| + | |||
=Beispiele= | =Beispiele= | ||
| Zeile 111: | Zeile 120: | ||
| Nach 6.: | | Nach 6.: | ||
ca. 12 (die Hälfte von 20 -25) | ca. 12 (die Hälfte von 20 -25) | ||
| − | | 3/4 ( | + | | 3/4 (75%) |
| <div align="right">9</div> | | <div align="right">9</div> | ||
|- | |- | ||
| Zeile 117: | Zeile 126: | ||
| Nach 6.: | | Nach 6.: | ||
ca. 11 (die Hälfte von 20 -25) | ca. 11 (die Hälfte von 20 -25) | ||
| − | | 3/4 ( | + | | 3/4 (75%) |
| <div align="right">8</div> | | <div align="right">8</div> | ||
|- | |- | ||
| Zeile 150: | Zeile 159: | ||
= 11+14 | = 11+14 | ||
= 25 | = 25 | ||
| − | |3/4 | + | |3/4 (75%) |
|<div align="right">17</div> | |<div align="right">17</div> | ||
|- | |- | ||
|[[Datei:KlpA.gif]] | |[[Datei:KlpA.gif]] | ||
|Schon gelaufen | |Schon gelaufen | ||
| − | | 1 | + | | 1/1 (100%) |
|<div align="right">25</div> | |<div align="right">25</div> | ||
|- | |- | ||
| Zeile 176: | Zeile 185: | ||
|Nach 2.: | |Nach 2.: | ||
11 + 3/4 * 25 | 11 + 3/4 * 25 | ||
| − | |1/3 | + | |1/3 (33%) |
|<div align="right">15</div> | |<div align="right">15</div> | ||
|- | |- | ||
| Zeile 212: | Zeile 221: | ||
Der Erwartungswert wird allerdings etwas höher liegen aufgrund der kleinen Karten in [[Datei:Pik.gif]]/[[Datei:Kreuz.gif]] und der [[Trumpflänge]]. | Der Erwartungswert wird allerdings etwas höher liegen aufgrund der kleinen Karten in [[Datei:Pik.gif]]/[[Datei:Kreuz.gif]] und der [[Trumpflänge]]. | ||
| + | =Praxistip= | ||
| + | |||
| + | Tatsächlich braucht es sehr viel Praxis auf diese Art und Weise den Erwartungswert festzustellen, deshalb kann man folgende Faustregel anlegen: | ||
| + | |||
| + | * Eine schwarze Farbe frei = 50 | ||
| + | * Schwarze Farbe in der ersten Runde = 25 | ||
| + | * Schwarze Farbe in der zweiten Runde = 15 | ||
| + | * Herz in der ersten Runde = 15 | ||
| + | * Herz 10 = 25 | ||
| + | * Jede schwarze Dame = 10 Punkte | ||
| + | |||
| + | Auf diese Art und Weise kann man sehr schnell einen groben Überblick über seine Stärke bekommen. Man sieht vor allem dass folgendes Blatt nicht zum eigenständigen Re taugt, weil der Erwartungswert <50 ist. Wenn der Partner die schwarzen Asse spielt und Re gibt, sieht das natürlich ganz anders aus und man kann die 90 sagen. | ||
| + | |||
| + | [[Datei:Klh10.gif]][[Datei:KlkD.gif]][[Datei:KlpD.gif]][[Datei:KlhD.gif]][[Datei:KlpB.gif]][[Datei:KlpB.gif]][[Datei:KlhB.gif]][[Datei:Klp10.gif]][[Datei:KlpK.gif]][[Datei:KlkK.gif]][[Datei:KlkK.gif]][[Datei:Klh9.gif]] | ||
| + | Anders herum kann bei zwei lauffähigen schwarzen Assen, [[Datei:KlkD.gif]] (60) und Dulle oder beide [[Datei:KlpD.gif]] schon Re angesagt werden. | ||
| + | =Sonderfall Solo= | ||
| + | Hier : | ||
| + | http://www.doko-non-stopp.de/tabellen_der_erwartungswerte_bei.htm | ||
| + | findet sich eine hervorragende Tabelle um das für ein Solo zu berechnen. | ||
| + | [[Category:Praxis]] | ||
[[Kategorie: DokoLexikon]] | [[Kategorie: DokoLexikon]] | ||
Aktuelle Version vom 29. Juni 2009, 12:53 Uhr
Quelle:ES 2.1.1
Die Stärke des eigenen Blattes wird am besten ausgedrückt durch eine durchschnittlich damit erreichbare Augenzahl. Die Berechnung dieser Augenzahl erfolgt über die Abschätzung von Erwartungswerten für potentielle Stiche.
Wieviel Augen ist eine Dulle im Durchschnitt wert? Wieviel Augen mache ich normal, wenn ich ![]() oder
oder ![]() frei bin Chicane?
frei bin Chicane?
Der Erwartungswert ist das Produkt aus dem Wert eines Stiches und der Wahrscheinlichkeit diesen Stich tatsächlich zu erhalten. Erwartungswerte helfen bei der Abschätzung, ob man als erster Re oder kontra ansagen soll/kann/muss.
Die folgende Tabelle zeigt ein einfaches Schema zur Abschätzung dieser Werte. (vgl. Mindestblattstärke für eine Erstansage)
Inhaltsverzeichnis
Tabelle
Tab. 2: Erwartungswerte für potentielle Stiche
| Nr. | Potentieller Stich | Wert des Stiches | Wahrscheinlichkeit des
Stiches |
|---|---|---|---|
| 1 | Stechen von ersten Lauf (Chicane) |
= eigene Stechkarte + 20
(genauer: angespieltes As + 2/7 der restlichen Augenzahl der Farbe) |
9/10 (Anmerkung: vgl. Lauf von Fehlkarten) |
| 2 | Stechen von zweiten Lauf (Singleton) |
= eigene Stechkarte + 10 bis 25
Beachte: Der Wert hängt stark vom ersten Lauf ab |
1/2 (bei Chicane = 2/3)
Beachte: Die Wahrscheinlichkeit wird durch den ersten Lauf beinflusst. |
| 3 | Stechen von Lauf (Chicane) |
= eigene Stechkarte + 15
(genauer: angespieltes As + 2/5 der restlichen Augenzahl der Farbe) |
3/4 |
| 4 | Besitz von |
~20 - 30 (hängt von der
Möglichkeit des Einsatzes der Karte ab) | |
| 5 | Besitz von |
~ 15 - 20 (in Kombination mit |
3/4 (Schätzung) |
| 6 | Besitz von |
~ » 20 - 25 (in Kombination mit Weitere Damen erhöhen diesen
Wert nur noch geringfügig.
Genauso sind einzelne |
3/4 (Schätzung) |
| 7 | Anspielasse:
Anmerkung: + bezieht sich auf die sonstigen Handkarten in dieser Farbe
also: z.B: |
für = 11 + 3/Anzahl der fehlenden
Karten der Farbe x (50 - eigene
Augenzahl der Farbe)
für |
Die Angaben gelten nur für ein As. Das nächste As läuft mit dem Produkt der Werte der Einzelwahrscheinlichkeiten. |
Beispiele
Quelle: Essener System (ES 2.1.1) Seite 9 ff.
Blatt 1
![]() wurde bereits Aufgespielt. Der Stich (z.B.
wurde bereits Aufgespielt. Der Stich (z.B. ![]()
![]()
![]()
![]() ) brachte 25 Augen.
) brachte 25 Augen.
Die Berechnung ist etwas unübersichtlich...Daher nochmal ganz genau:
- 11 = Das ist der Augen-Wert der Karte (
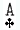 )
) - 3/6 = 3(fester Wert) / 6 (2 Kreuz-Karten auf der Hand. Also 8 - 2 = 6 Karten im Spiel)
- (50-22) = 50 (fester Wert) - 22 (
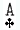
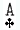 auf der Hand = 2 x 11 Augen = 22)
auf der Hand = 2 x 11 Augen = 22)
Blatt 2
mögliche Stiche:
- 1)
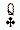 = 3/4 * 17,5 ~ 13
= 3/4 * 17,5 ~ 13 - 2) Stechen 1.
 -Lauf: 3/4 x (10 + 15) ~ 19 (Chicane)
-Lauf: 3/4 x (10 + 15) ~ 19 (Chicane) - 3) Stechen 2.
 /
/ -Lauf: 1/2 x (4 + 17,5) + 1/2 x (2 + 17,5) = 20,5 (Single)
-Lauf: 1/2 x (4 + 17,5) + 1/2 x (2 + 17,5) = 20,5 (Single)
Summe = 13 + 19 + 20,5 = 52,5
Der Erwartungswert wird allerdings etwas höher liegen aufgrund der kleinen Karten in ![]() /
/![]() und der Trumpflänge.
und der Trumpflänge.
Praxistip
Tatsächlich braucht es sehr viel Praxis auf diese Art und Weise den Erwartungswert festzustellen, deshalb kann man folgende Faustregel anlegen:
- Eine schwarze Farbe frei = 50
- Schwarze Farbe in der ersten Runde = 25
- Schwarze Farbe in der zweiten Runde = 15
- Herz in der ersten Runde = 15
- Herz 10 = 25
- Jede schwarze Dame = 10 Punkte
Auf diese Art und Weise kann man sehr schnell einen groben Überblick über seine Stärke bekommen. Man sieht vor allem dass folgendes Blatt nicht zum eigenständigen Re taugt, weil der Erwartungswert <50 ist. Wenn der Partner die schwarzen Asse spielt und Re gibt, sieht das natürlich ganz anders aus und man kann die 90 sagen.
Anders herum kann bei zwei lauffähigen schwarzen Assen, ![]() (60) und Dulle oder beide
(60) und Dulle oder beide ![]() schon Re angesagt werden.
schon Re angesagt werden.
Sonderfall Solo
Hier :
http://www.doko-non-stopp.de/tabellen_der_erwartungswerte_bei.htm
findet sich eine hervorragende Tabelle um das für ein Solo zu berechnen.