Version vom 14. Mai 2009, 17:11 Uhr

Quelle:ES 2.1.1

Erwartungswerte werden vor einer Erstansage ermittelt. (vgl. Mindestblattstärke für eine Erstansage)

Tabelle

Tab. 2: Erwartungswerte für potentielle Stiche

Nr.	Potentieller Stich	Wert des Stiches	Wahrscheinlichkeit des Stiches
1	Stechen von oder beim ersten Lauf (Chicane)	= eigene Stechkarte + 20 (genauer: angespieltes As + 2/7 der restlichen Augenzahl der Farbe)	9/10 (Anmerkung: vgl. Lauf von Fehlkarten)
2	Stechen von oder beim zweiten Lauf (Singleton)	= eigene Stechkarte + 10 bis 25 Beachte: Der Wert hängt stark vom ersten Lauf ab	1/2 (bei Chicane = 2/3) Beachte: Die Wahrscheinlichkeit wird durch den ersten Lauf beinflusst.
3	Stechen von beim ersten Lauf (Chicane)	= eigene Stechkarte + 15 (genauer: angespieltes As + 2/5 der restlichen Augenzahl der Farbe)	3/4
4	Besitz von	~20 - 30 (hängt von der Möglichkeit des Einsatzes der Karte ab)
5	Besitz von	~ 15 - 20 (in Kombination mit sinkt der Wert auf ca.10 -15)	3/4 (Schätzung) In Kombination mit steigt die Wahrscheinlichkeit auf ~ 1.
6	Besitz von +	~ » 20 - 25 (in Kombination mit sinkt der Wert auf ca 15 - 20) Weitere Damen erhöhen diesen Wert nur noch geringfügig. Genauso sind einzelne und / allein nur von sehr geringem Wert.	3/4 (Schätzung) In Kombination mit steigt die Wahrscheinlichkeit auf ~ 1.
7	Anspielasse: oder + 0 oder + 1 oder + 2 entsp. oder + 3 entsp. +1 oder + 4 entsp. +2 Anmerkung: + bezieht sich auf die sonstigen Handkarten in dieser Farbe also: z.B: +	für oder : = 11 + 3/Anzahl der fehlenden Karten der Farbe x (50 - eigene Augenzahl der Farbe) für : = 11 + 3/Anzahl der fehlenden Karten der Farbe x (30 - eigene Augenzahl der Farbe)	9/10 (nach Ansage = 9/10) 3/4 (nach Ansage = 9/10) 2/3 (nach Ansage = 3/4) 1/2 (nach Ansage = 2/3) 1/4 (nach Ansage = 1/2) Die Angaben gelten nur für ein As. Das nächste As läuft mit dem Produkt der Werte der Einzelwahrscheinlichkeiten.

Beispiele

Quelle: Essener System (ES 2.1.1) Seite 9 ff.

Blatt 1

wurde bereits Aufgespielt. Der Stich (z.B. ) brachte 25 Augen.

Handkarte	Wert der Karte	Multiplikator (Wahrscheinlichkeit)	~ endgültiger Wert
	Nach 6.: ca. 12 (die Hälfte von 20 -25)	3/4 (75%)	9
	Nach 6.: ca. 11 (die Hälfte von 20 -25)	3/4 (75%)	8
			0
			0
			0
			0
			0
	Nach 7.: 11 + 3/6 * (50-22) = 11+14 = 25	3/4 (75%)	17
	Schon gelaufen	1/1 (100%)	25
			0
			0
			0
Single	Nach 2.: 11 + 3/4 * 25	1/3 (33%)	15
Summe:			76

Anmerkung zur Karte

Die Berechnung ist etwas unübersichtlich...Daher nochmal ganz genau:

• 11 = Das ist der Augen-Wert der Karte ()
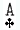• 3/6 = 3(fester Wert) / 6 (2 Kreuz-Karten auf der Hand. Also 8 - 2 = 6 Karten im Spiel)
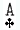
• (50-22) = 50 (fester Wert) - 22 ( 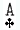auf der Hand = 2 x 11 Augen = 22)

Blatt 2

mögliche Stiche:

• 1) 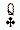= 3/4 * 17,5 ~ 13
• 2) Stechen 1.-Lauf: 3/4 x (10 + 15) ~ 19 (Chicane)
• 3) Stechen 2. /-Lauf: 1/2 x (4 + 17,5) + 1/2 x (2 + 17,5) = 20,5 (Single)

Summe = 13 + 19 + 20,5 = 52,5

Der Erwartungswert wird allerdings etwas höher liegen aufgrund der kleinen Karten in / und der Trumpflänge.

Praxistip

Tatsächlich braucht es sehr viel Praxis auf diese Art und Weise den Erwartungswert festzustellen, deshalb kann man folgende Faustregel anlegen:

• Eine schwarze Farbe frei = 50
• Schwarze Farbe in der ersten Runde = 25
• Schwarze Farbe in der zweiten Runde = 15
• Herz in der ersten Runde = 15
• Herz 10 = 25
• Jede schwarze Dame = 10 Punkte

Auf diese Art und Weise kann man sehr schnell eine Überblick bekommen. Man sieht vor allem dass folgendes Blatt nicht zum eigenständigen Re taugt, weil der Erwartungswert <50 ist. Wenn der Partner die schwarzen Asse spielt und Re gibt, sieht das natürlich ganz anders aus und man kann die 90 sagen.

Anders herum kann bei zwei lauffähigen schwarzen Assen, (60) und Dulle oder beide schon Re angesagt werden.