Essener System: Unterschied zwischen den Versionen
Solmyr (Diskussion | Beiträge) K (→Stärke der Erstansage: aufgehübscht) |
|||
| (24 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | http://de.wikipedia.org/wiki/Essener_System | + | Quelle siehe: http://de.wikipedia.org/wiki/Essener_System |
| + | |||
| + | Weblink: http://mwolff.info/Essener_System.pdf | ||
Die hier dargestellten Textpassagen sind Auszüge aus den oben genannten Original... | Die hier dargestellten Textpassagen sind Auszüge aus den oben genannten Original... | ||
| Zeile 6: | Zeile 8: | ||
Vielleicht findet sich noch jemand der die Beispiele und Tabellen einbauen kann... | Vielleicht findet sich noch jemand der die Beispiele und Tabellen einbauen kann... | ||
| + | ---- | ||
| + | |||
| + | '''Vorwort''' | ||
| + | |||
| + | Liebe Doppelkopffreunde! | ||
| + | |||
| + | Jeder von Euch kennt zumindest dem Namen nach noch eine ganze Reihe weitere Kartenspiele, wie zum Beispiel Bridge, Skat, Uno, Romme, Mau-Mau, Poker u.v.a.. Warum hat ausgerechnet Doppelkopf in Euch und uns so begeisterte Anhänger gefunden? Die Gründe liegen sicherlich darin, daß Doppelkopf zu den spieltechnisch und strategisch anspruchsvollsten Kartenspielen zu zählen ist und, daß Doppelkopf ein Partnerspiel ist. | ||
| + | |||
| + | Das Spielziel beim Turnierdoppelkopf besteht darin, zusammen mit verschiedenen Partnern so viele Spiele so hoch wie möglich zu gewinnen. Mitentscheidend hierfür ist in jedem Spiel das Verständnis mit dem jeweiligen Spielpartner. Je mehr Informationen hinsichtlich der Stärke und Struktur der Blätter man austauschen kann, desto leichter fällt es einen optimalen Spielplan für die eigene Partei zu finden und somit ein Maximum an Spielpunkten zu sammeln. Hierbei müssen selbstverständlich die Spielregeln und die Regeln des Fair Play eingehalten werden. Aktionen wie zum Beispiel "Wenn ich mit links ausspiele bin ich KONTRA-Spieler und wenn ich mit rechts ausspiele bin ich RE-Spieler" oder nicht regelgerechte Aussprüche wie zum Beispiel "Hallo Partner, ich mach den Stich" sind selbstverständlich zu verurteilen. Trotzdem ist es möglich regelgerecht detaillierte Informationen auszutauschen. Beispiele hierzu hat Bernhard Kopp in seinem Buch "Gewinnen beim Doppelkopf" gegeben. Wir erinneren nur an die Bedeutungen von Ansagezeitpunkten, 90-Anfragen und einigen Konventionen (As-Signal, Farbvorzugsignal bei As-Soli oder Hoch-Niedrig-Markierungen bei Normalspielen). | ||
| + | |||
| + | Warum also nun dieses Ausarbeitung? Hierfür gibt es mehrere Gründe: Das Doppelkopfspiel hat in der Zwischenzeit eine rasante Weiterentwicklung erfahren. Inspiriert durch Berhard's Buch, ist das Doppelkopfspiel mit vielen neuen Ideen bereichert worden. Leider haben unsere persönlichen Erfahrungen gezeigt, daß diese neuen (und auch einige alte) Ideen zur Informationsübermittlung nur wenigen Insidern bekannt sind bzw. nur von wenigen Doppelkopffreunden in ihrer Gesamtheit verstanden und korrekt angewendet werden. Ein prägnantes Beispiel in diesem Zusammenhang ist sicherlich die Dullenkonvention (Vorspiel der [[Datei:Klh10.gif]] bis zum dritten Stich). Zudem fehlt es an einem logischen Gesamtkonzept für die regelgerechte Kommunikation zwischen den Spielpartnern. | ||
| + | |||
| + | In dieser Ausarbeitung stellen wir daher ein umfangreiches, auf Logik aufbauendes Kommunikationssystem vor, daß sich zum größten Teil in der Praxis bereits hervorragend bewährt hat und zu einem kleinen Teil vollkommen neue Aspekte enthält, die in der Praxis noch erprobt werden müssen. Wir haben es aufgrund unserer Vereinszugehörigkeit zur "Geknickten Dulle Essen 88 e.V." kurz das "Essener System" genannt. Im wesentlichen beantworten wir folgende Fragen: | ||
| + | |||
| + | * Wann bzw. unter welchen Bedingungen ist ein Austausch von Informationen überhaupt sinnvoll ? | ||
| + | * Welche regelgerechten "Hilfsmittel" stehen dem Doppelkopfspieler zur Informationsübermittlung zur Verfügung? | ||
| + | * Welche Regeln gelten für ihre Anwendung? | ||
| + | * Wie hängt die Interpretation des angewendeten Hilfsmittels von der speziellen Spielsituation ab? | ||
| + | |||
| + | Wir würden uns freuen, wenn Ihr uns nach einer kritischen Auseinandersetzung mit dieser Ausarbeitung Eure Beobachtungen hinsichtlich Mängel oder Verbesserungsvorschlägen zukommen laßt. Unser besonderer Dank gilt Ralf Schmidt (MG 1MDV) für seine Hinweise zur vorletzten Fassung und Michael Remme (E GD88) für das Layout des Titelblattes. Ferner danken wir allen Doppelkopffreunden, die uns in den letzten zwei Jahren direkt oder indirekt dazu ermuntert haben, unsere Spielweise schriftlich zu fixieren. | ||
| + | |||
| + | Viel Spaß beim Lesen und Nachspielen der angegebenen Beispiele wünschen Euch | ||
| + | '''Claus Günther, Jörg Passenberg und Heinz Zedler''' | ||
| − | |||
(...) | (...) | ||
| + | |||
| Zeile 16: | Zeile 41: | ||
Das Primärziel jedes erfolgsuchenden Dokospielers ist sicherlich aus den eigenen Karten und | Das Primärziel jedes erfolgsuchenden Dokospielers ist sicherlich aus den eigenen Karten und | ||
den Kartenverteilungen die optimale Punktausbeute zu erzielen. Ein Teilaspekt ist hierbei die | den Kartenverteilungen die optimale Punktausbeute zu erzielen. Ein Teilaspekt ist hierbei die | ||
| − | optimale | + | optimale Ausreizung der Blätter der eigenen Partnerschaft. Hierbei vor allem soll das Essener |
System behilflich sein, indem es im wesentlichen die Sicherheit von Ansagen (inkl. Gegenansagen) | System behilflich sein, indem es im wesentlichen die Sicherheit von Ansagen (inkl. Gegenansagen) | ||
erhöht. Dies geschieht dadurch, daß dem Ansagenden zum Zeitpunkt seiner Ansage, der ja | erhöht. Dies geschieht dadurch, daß dem Ansagenden zum Zeitpunkt seiner Ansage, der ja | ||
| Zeile 61: | Zeile 86: | ||
! width="250px" | Wahrscheinlichkeitserhöhung für Gegenansagen | ! width="250px" | Wahrscheinlichkeitserhöhung für Gegenansagen | ||
|- | |- | ||
| − | | | + | |RE/KONTRA |
|>=50,00% | |>=50,00% | ||
|>=18,18% | |>=18,18% | ||
| Zeile 85: | Zeile 110: | ||
(ohne die Gegenansage) Ansage eine Wahrscheinlichkeit von 100% besitzt. Weiterhin dienen | (ohne die Gegenansage) Ansage eine Wahrscheinlichkeit von 100% besitzt. Weiterhin dienen | ||
Ansagen als (i.d.R. positive) Antworten auf Anfragen des Partners. | Ansagen als (i.d.R. positive) Antworten auf Anfragen des Partners. | ||
| − | |||
== Wahl des Ansagezeitpunktes == | == Wahl des Ansagezeitpunktes == | ||
''' | ''' | ||
| − | Es gilt folgendes Grundprinzip:''' | + | Es gilt folgendes Grundprinzip:''' |
Jeder Ansagezeitpunkt, der nicht mit dem letztmöglichen Zeitpunkt für die | Jeder Ansagezeitpunkt, der nicht mit dem letztmöglichen Zeitpunkt für die | ||
| Zeile 110: | Zeile 134: | ||
Sie dient bei ungeklärter eigener Parteizugehörigkeit i.d.R. zur Partnerschaftsklärung (Man gibt | Sie dient bei ungeklärter eigener Parteizugehörigkeit i.d.R. zur Partnerschaftsklärung (Man gibt | ||
sich dem Anspielenden, dem vermutlichen bzw. sicheren Partner zu erkennen). Ist die eigene | sich dem Anspielenden, dem vermutlichen bzw. sicheren Partner zu erkennen). Ist die eigene | ||
| − | Parteizugehörigkeit geklärt, so soll sie den Anspielenden (Partner) vom Normalanspiel abbringen. | + | Parteizugehörigkeit geklärt, so soll sie den Anspielenden (Partner) vom [[Normalanspiel]] abbringen. |
Was verstehen wir unter Normalanspiel? Es ist das Anspiel, welches in der jeweiligen | Was verstehen wir unter Normalanspiel? Es ist das Anspiel, welches in der jeweiligen | ||
Spielsituation (ohne die Ansage) das objektiv beste ist. Bei dieser Beurteilung darf der Anspielende | Spielsituation (ohne die Ansage) das objektiv beste ist. Bei dieser Beurteilung darf der Anspielende | ||
| Zeile 137: | Zeile 161: | ||
=== (Anspiel-)Konventionen === | === (Anspiel-)Konventionen === | ||
| − | Hiermit sind Anspiele (bis zum letztmöglichen Ansagezeitpunkt) gemeint, die, je nach Verknüpfung | + | Hiermit sind Anspiele (bis zum letztmöglichen Ansagezeitpunkt) gemeint, die, je nach Verknüpfung mit den Hilfsmitteln 1-3, jeweils immer denselben Informationsgehalt (inkl. Parteizugehörigkeit) besitzen. Sie erfordern häufig eine spezifische Reaktion des Partners. Eine sinnvolle Konvention muß folgende Anforderungen erfüllen: |
| − | mit den Hilfsmitteln 1-3, jeweils immer denselben Informationsgehalt (inkl. Parteizugehörigkeit) | ||
| − | besitzen. Sie erfordern häufig eine spezifische Reaktion des Partners. Eine sinnvolle Konvention | ||
| − | muß folgende Anforderungen erfüllen: | ||
| − | * Die mit ihr verbundene Information muß auf Dauer für die eigene Partei mehr Vorteile | + | * Die mit ihr verbundene Information muß auf Dauer für die eigene Partei mehr Vorteile bringen (Steigerung des Erwartungswertes) als eine, durch das Anspiel verursachte, eventuelle Schwächung des eigenen Blattes. |
| − | bringen (Steigerung des Erwartungswertes) als eine, durch das Anspiel verursachte, | + | * Sie muß logisch aufgebaut sein, damit es bei den Folgereaktionen nicht zu Mißverständnissen kommt und damit auch unkundige Spieler sie nachvollziehen können. |
| − | eventuelle Schwächung des eigenen Blattes. | ||
| − | * Sie muß logisch aufgebaut sein, damit es bei den Folgereaktionen nicht zu Mißverständnissen | ||
| − | kommt und damit auch unkundige Spieler sie nachvollziehen können. | ||
* Die Wahrscheinlichkeit der Anwendung muß genügend groß sein. | * Die Wahrscheinlichkeit der Anwendung muß genügend groß sein. | ||
* Die Anfälligkeit gegen Störmanöver der Gegenpartei muß gering sein. | * Die Anfälligkeit gegen Störmanöver der Gegenpartei muß gering sein. | ||
| − | Die folgenden Kapitel zeigen nun, geordnet nach Spieltypen (Normalspiel; Hochzeit; Solo), welche | + | Die folgenden Kapitel zeigen nun, geordnet nach Spieltypen (Normalspiel; Hochzeit; Solo), welche zusätzlichen Möglichkeiten das Doppelkopfspiel durch Verwendung dieser Hilfsmittel erhält. Dabei werden wir immer versuchen anhand von praktischen Beispielen die Ideen dieses Systems und seine Logik anschaulich darzulegen. Selbstverständlich werden wir hinsichtlich der exakten Bedeutung der Hilfsmittel (beispielsweise: Konventionen und Ansagen zum Abbringen vom Normalanspiel) in Abhängigkeit von der genauen Situation unsere eigenen Vorlieben vorstellen. Seid uns also nicht böse, wenn andere Interpretationen nicht zu Wort kommen werden. |
| − | zusätzlichen Möglichkeiten das Doppelkopfspiel durch Verwendung dieser Hilfsmittel erhält. | ||
| − | Dabei werden wir immer versuchen anhand von praktischen Beispielen die Ideen dieses Systems | ||
| − | und seine Logik anschaulich darzulegen. Selbstverständlich werden wir hinsichtlich der exakten | ||
| − | Bedeutung der Hilfsmittel (beispielsweise: Konventionen und Ansagen zum Abbringen vom | ||
| − | Normalanspiel) in Abhängigkeit von der genauen Situation unsere eigenen Vorlieben vorstellen. | ||
| − | Seid uns also nicht böse, wenn andere Interpretationen nicht zu Wort kommen werden. | ||
=Normalspiel = | =Normalspiel = | ||
| Zeile 162: | Zeile 174: | ||
Ein Normalspiel ist durch die folgenden Eigenschaften definiert: | Ein Normalspiel ist durch die folgenden Eigenschaften definiert: | ||
| − | *Eine eindeutige Klärung der Partnerschaften erfolgt durch Ansagen oder Legen der [[Datei:KlkD.gif]], | + | *Eine eindeutige Klärung der Partnerschaften erfolgt durch Ansagen oder Legen der [[Datei:KlkD.gif]], d. h. der Zeitpunkt der Klärung ist nicht festgelegt. |
| − | d. h. der Zeitpunkt der Klärung ist nicht festgelegt. | ||
* Die letztmöglichen Ansagezeitpunkte sind unabhängig vom Spielverlauf. | * Die letztmöglichen Ansagezeitpunkte sind unabhängig vom Spielverlauf. | ||
| − | Andere Spieltypen sind Hochzeiten (Kap. 3) und Soli (Kap. 4). Eine Unterscheidung dieser Typen | + | Andere [[Spieltypen]] sind Hochzeiten (Kap. 3) und Soli (Kap. 4). Eine Unterscheidung dieser Typen erscheint sinnvoll, da die vorzeitige Information wer zusammenspielt (vor dem letztmöglichen Ansagezeitpunkt) einen großen Einfluß auf z. B. das Ansageverhalten haben kann. |
| − | erscheint sinnvoll, da die vorzeitige Information wer zusammenspielt (vor dem letztmöglichen | ||
| − | Ansagezeitpunkt) einen großen Einfluß auf z. B. das Ansageverhalten haben kann. | ||
== Erstansage == | == Erstansage == | ||
| Zeile 211: | Zeile 220: | ||
zweiten Lauf ([[Single|Singleton]]) | zweiten Lauf ([[Single|Singleton]]) | ||
|= eigene Stechkarte + 10 bis 25 | |= eigene Stechkarte + 10 bis 25 | ||
| − | Beachte: Der Wert hängt stark | + | Beachte: Der Wert hängt stark |
| − | + | vom ersten Lauf ab | |
|1/2 (bei Chicane = 2/3) | |1/2 (bei Chicane = 2/3) | ||
Beachte: Die Wahrscheinlichkeit | Beachte: Die Wahrscheinlichkeit | ||
| Zeile 281: | Zeile 290: | ||
Statistische Auswertungen verschiedener Einladungsturniere (Deutschlandpokal Braunschweig 1991, [[Dodge]]-Mannschaftsturnier München 1992 und 1. Dullenknicken Essen 1993) haben gezeigt, daß ein Re-Spieler durchschnittlich eine Augenzahl von etwa 68 und ein Kontra-Spieler durchschnittlich eine Augenzahl von etwa 52 pro Spiel erzielt. Für eine Erstansage sollte der Gesamterwartungswert des eigenen Blattes zum einen so groß sein, daß mit einem knapp unter Durchschnitt liegenden Blatt des Partners die Gewinnwahrscheinlichkeit etwas mehr als 50% beträgt, und zum anderen sollte er im Hinblick auf weitere Ansagen größer als der durchschnittliche Erwartungswert eines Spielers der jeweiligen Partei sein. Hieraus folgt für die [[Mindestblattstärke für eine Erstansage]]: | Statistische Auswertungen verschiedener Einladungsturniere (Deutschlandpokal Braunschweig 1991, [[Dodge]]-Mannschaftsturnier München 1992 und 1. Dullenknicken Essen 1993) haben gezeigt, daß ein Re-Spieler durchschnittlich eine Augenzahl von etwa 68 und ein Kontra-Spieler durchschnittlich eine Augenzahl von etwa 52 pro Spiel erzielt. Für eine Erstansage sollte der Gesamterwartungswert des eigenen Blattes zum einen so groß sein, daß mit einem knapp unter Durchschnitt liegenden Blatt des Partners die Gewinnwahrscheinlichkeit etwas mehr als 50% beträgt, und zum anderen sollte er im Hinblick auf weitere Ansagen größer als der durchschnittliche Erwartungswert eines Spielers der jeweiligen Partei sein. Hieraus folgt für die [[Mindestblattstärke für eine Erstansage]]: | ||
| − | * RE: > 75 Augen und | + | * RE: >= 75 Augen und |
| − | * KONTRA: > 85 Augen. | + | * KONTRA: >= 85 Augen. |
Für die Entscheidung Ansage ja oder nein zählt die bis zur Ansage erzielte Augenzahl plus Summe der Einzelerwartungswerte (siehe Tab. 2). Hierdurch wird klar, daß es i.d.R. besser ist bis zum letztmöglichen Zeitpunkt mit der Ansage zu warten, da ansonsten Informationen, die eine Neuberechnung der Erwartungswerte bedingen, unnötigerweise verlorengehen. Es gibt nur zwei Ausnahmen: | Für die Entscheidung Ansage ja oder nein zählt die bis zur Ansage erzielte Augenzahl plus Summe der Einzelerwartungswerte (siehe Tab. 2). Hierdurch wird klar, daß es i.d.R. besser ist bis zum letztmöglichen Zeitpunkt mit der Ansage zu warten, da ansonsten Informationen, die eine Neuberechnung der Erwartungswerte bedingen, unnötigerweise verlorengehen. Es gibt nur zwei Ausnahmen: | ||
| Zeile 288: | Zeile 297: | ||
* Es wird Trumpf angespielt und der Ansagende legt [[Datei:Klh10.gif]] (Die Ansage erfolgt sofort, da keine Neubewertung möglich ist und der Partner die Gelegenheit zum Unterbringen von [[Datei:KlcA.gif]] oder [[Datei:Klc10.gif]] hat). | * Es wird Trumpf angespielt und der Ansagende legt [[Datei:Klh10.gif]] (Die Ansage erfolgt sofort, da keine Neubewertung möglich ist und der Partner die Gelegenheit zum Unterbringen von [[Datei:KlcA.gif]] oder [[Datei:Klc10.gif]] hat). | ||
| − | * Es liegen 2 [[ | + | * Es liegen 2 [[Volle]] und die Stechkarte ist ebenfalls ein Voller (Hier erfolgt ebenfalls sofort eine Ansage wegen der Chance auf einen Doko und der geringen Gefahr des Verlustes des |
Stiches [< 5%] ). | Stiches [< 5%] ). | ||
Nun aber zu einigen Blattbeispielen, die das Bewertungsschema etwas verdeutlichen sollen: (...) | Nun aber zu einigen Blattbeispielen, die das Bewertungsschema etwas verdeutlichen sollen: (...) | ||
| − | '' | + | '' Die Orginal Beispiele sind in einer "auhfgehübscht Form" zu finden unter:[[Erwartungswerte]]'' |
| − | Die Beispiele sollten zeigen, wie mit Hilfe des obigen Schemas die Blattstärke abgeschätzt wird. | + | Die Beispiele sollten zeigen, wie mit Hilfe des obigen Schemas die Blattstärke abgeschätzt wird. Gleichzeitig ist dabei auf einige Schwächen aufmerksam gemacht worden. Eine Einschätzung eines Wertes für Trumpflänge bzw. -kürze fehlt. Auch sind die Angaben für das Stechen von Farben relativ ungenau, da die Wahrscheinlichkeiten zum einen davon abhängen, was im ersten Stich in der Farbe gefallen ist und zum anderen davon abhängen, ob der betreffende Spieler eine Ansage getätigt hat (mit Ansage erhöhen sich die Wahrscheinlichkeiten etwas). Bei allen Bättern sollte die Erstansage zum letztmöglichen Zeitpunkt getroffen werden, da die volle Information des Spielverlaufes für die Entscheidung, ob überhaupt eine Erstansage getroffen werden kann, benötigt wird. Folgende Spielverläufe führen zu einer Abwertung der Blattstärke und können zum |
| − | Gleichzeitig ist dabei auf einige Schwächen aufmerksam gemacht worden. Eine Einschätzung | ||
| − | eines Wertes für Trumpflänge bzw. -kürze fehlt. Auch sind die Angaben für das Stechen von | ||
| − | Farben relativ ungenau, da die Wahrscheinlichkeiten zum einen davon abhängen, was im ersten | ||
| − | Stich in der Farbe gefallen ist und zum anderen davon abhängen, ob der betreffende Spieler eine | ||
| − | Ansage getätigt hat (mit Ansage erhöhen sich die Wahrscheinlichkeiten etwas). Bei allen Bättern | ||
| − | sollte die Erstansage zum letztmöglichen Zeitpunkt getroffen werden, da die volle Information des | ||
| − | Spielverlaufes für die Entscheidung, ob überhaupt eine Erstansage getroffen werden kann, | ||
| − | benötigt wird. Folgende Spielverläufe führen zu einer Abwertung der Blattstärke und können zum | ||
Verzicht einer Erstansage führen: | Verzicht einer Erstansage führen: | ||
* Das selbst angespielte As wird gestochen oder man wird überstochen. | * Das selbst angespielte As wird gestochen oder man wird überstochen. | ||
| − | * Der erste Lauf einer Farbe, die man im zweiten Lauf stechen will wird hinter dem Spieler | + | * Der erste Lauf einer Farbe, die man im zweiten Lauf stechen will wird hinter dem Spieler beim ersten Lauf gestochen oder es fällt direkt hinter dem Spieler das As (Verringerung der Wahrscheinlichkeit) oder der Stich wird extrem fett (Wert des zweiten Stiches sinkt). |
| − | beim ersten Lauf gestochen oder es fällt direkt hinter dem Spieler das As (Verringerung der | ||
| − | Wahrscheinlichkeit) oder der Stich wird extrem fett (Wert des zweiten Stiches sinkt). | ||
| − | * Ein anderer Spieler macht die ersten beiden Stiche: Hierdurch sinkt der durchschnittliche | + | * Ein anderer Spieler macht die ersten beiden Stiche: Hierdurch sinkt der durchschnittliche Wert des Partnerblattes, da der Spieler mit höherer Wahrscheinlichkeit Gegner ist (besonders wenn der Spieler RE ansagen wollte). Daraus folgt: Für eine Erstansage ist ein stärkeres Blatt erforderlich. |
| − | Wert des Partnerblattes, da der Spieler mit höherer Wahrscheinlichkeit Gegner ist | ||
| − | (besonders wenn der Spieler RE ansagen wollte). Daraus folgt: Für eine Erstansage ist ein | ||
| − | stärkeres Blatt erforderlich. | ||
* Es erfolgt eine Ansage der Gegenpartei vor der eigenen Ansage (siehe Kap. 2.3). | * Es erfolgt eine Ansage der Gegenpartei vor der eigenen Ansage (siehe Kap. 2.3). | ||
| Zeile 321: | Zeile 317: | ||
In besondern Situationen kann eine Erstansage auch mit Blättern erfolgen, die knapp unter den Erfordernissen für eine Erstansage liegen. Hierzu ist allerdings notwendig, daß der Spieler zu diesem sehr frühen Zeitpunkt abschätzen kann, daß alle anderen Spieler ein ungefähr gleich starkes Blatt halten und somit sein eigenes Blatt, welches nur noch knapp über dem Durchschnitt liegt zum Gewinn ausreichen sollte. Die Gefahr bei einer solchen Ansage ist allerdings, daß der Partner mit einem wesentlichen stärkeren Blatt rechnet und somit eine weitere Ansage trifft. | In besondern Situationen kann eine Erstansage auch mit Blättern erfolgen, die knapp unter den Erfordernissen für eine Erstansage liegen. Hierzu ist allerdings notwendig, daß der Spieler zu diesem sehr frühen Zeitpunkt abschätzen kann, daß alle anderen Spieler ein ungefähr gleich starkes Blatt halten und somit sein eigenes Blatt, welches nur noch knapp über dem Durchschnitt liegt zum Gewinn ausreichen sollte. Die Gefahr bei einer solchen Ansage ist allerdings, daß der Partner mit einem wesentlichen stärkeren Blatt rechnet und somit eine weitere Ansage trifft. | ||
| − | Daher sollte von diesem Typ der Ansage nur sehr spärlich an Position 3 oder 4 (verringert das | + | Daher sollte von diesem Typ der Ansage nur sehr spärlich an Position 3 oder 4 (verringert das Risiko einer weiteren Ansage des Partners) Gebrauch gemacht werden. Ein Beispiel: |
| − | Risiko einer weiteren Ansage des Partners) Gebrauch gemacht werden. Ein Beispiel: | ||
| − | Blatt 1: | + | Blatt 1: [[Datei:Klh10.gif]] [[Datei:KlkD.gif]][[Datei:KlpD.gif]] [[Datei:KlkB.gif]][[Datei:KlpB.gif]] [[Datei:Klc10.gif]][[Datei:Klk10.gif]][[Datei:Klk9.gif]] [[Datei:KlpA.gif]][[Datei:KlhA.gif]][[Datei:KlhA.gif]] (Position 2) |
| − | 1.Stich: | + | 1.Stich: [[Datei:KlkK.gif]][[Datei:Klk10.gif]][[Datei:KlkA.gif]][[Datei:Klk9.gif]] |
| − | 2.Stich: | + | 2.Stich: [[Datei:Klk10.gif]][[Datei:Klk9.gif]]+RE <[[Datei:KlkK.gif]]>[[Datei:KlkA.gif]] |
| + | |||
| + | Anmerkung: "<>" = Aufspiel --[[Benutzer:Solmyr|Solmyr]] 15:22, 24. Apr. 2009 (CEST) | ||
Nach der bisherigen Blattbewertung besitzt Spieler 2 kein Blatt für eine Erstansage | Nach der bisherigen Blattbewertung besitzt Spieler 2 kein Blatt für eine Erstansage | ||
| − | (Erwartungswert | + | (Erwartungswert > 68). In dieser besonderen Situation sollte Spieler 2 allerdings aus |
folgender Überlegungen trotzdem RE ansagen: Mit Spieler 1 oder 3 als Partner hat die | folgender Überlegungen trotzdem RE ansagen: Mit Spieler 1 oder 3 als Partner hat die | ||
| − | eigene Partei schon einen Stich, wobei Spieler 1 zusätzlich noch in | + | eigene Partei schon einen Stich, wobei Spieler 1 zusätzlich noch in [[Datei:Pik.gif]] [[Anschub|anschieben]] kann. Außerdem scheint keiner der Spieler ein über ein starkes Blatt zu verfügen (keine Ansage). |
| − | Außerdem scheint keiner der Spieler ein über ein starkes Blatt zu verfügen (keine | ||
| − | Ansage). | ||
Bei stärkeren als den bisher beschriebenen Blättern sieht die Situation anders aus: Stärkere | Bei stärkeren als den bisher beschriebenen Blättern sieht die Situation anders aus: Stärkere | ||
| − | Blätter sind immer gekennzeichnet durch Trumpflänge ( | + | Blätter sind immer gekennzeichnet durch Trumpflänge (>= 8 = wenige Fehlverlierer) und [[Trumpfstärke]] (Minimum: ~ [[Datei:KlkD.gif]][[Datei:KlpD.gif]][[Datei:KlcD.gif]][[Datei:KlcD.gif]] oder [[Datei:KlkD.gif]][[Datei:KlpD.gif]][[Datei:KlpD.gif]] oder bei Kontra-Partei [[Datei:Klh10.gif]][[Datei:KlpD.gif]][[Datei:KlhD.gif]][[Datei:KlhD.gif]]). |
| − | (Minimum: | ||
| − | '''Die Zahl 8 als Definition für [[Trumpflänge]]''' kommt dadurch zustande, daß die Wahrscheinlichkeit, daß kein anderer Spieler eine gleiche oder höhere Trumpfanzahl als dieser Spieler besitzt gerade bei | + | '''Die Zahl 8 als Definition für [[Trumpflänge]]''' kommt dadurch zustande, daß die Wahrscheinlichkeit, daß kein anderer Spieler eine gleiche oder höhere Trumpfanzahl als dieser Spieler besitzt gerade bei 8 Trumpf über 50% liegt. Eine Abschätzung nach dem bekannten Schema ist nur bedingt möglich, da die Trumpfstärke nur ungenau in eine durchschnittliche Augenzahl umgerechnet werden kann. Sie sollte aber für einen Re-Spieler bei > 100 und bei einem KONTRA-Spieler > 110 liegen. Besser erscheint in diesem Zusammenhang eine [[Verliererrechnung]]]. |
| − | 8 Trumpf über 50% liegt. Eine Abschätzung nach dem bekannten Schema ist nur bedingt möglich, da die Trumpfstärke nur ungenau in eine durchschnittliche Augenzahl umgerechnet werden kann. Sie sollte aber für einen Re-Spieler bei > 100 und bei einem KONTRA-Spieler > 110 liegen. Besser erscheint in diesem Zusammenhang eine [[Verliererrechnung]]]. | ||
Ein starkes Blatt sollte maximal 4 Verlierer besitzen. Wir unterscheiden zwischen ganzen und halben Verlierern: | Ein starkes Blatt sollte maximal 4 Verlierer besitzen. Wir unterscheiden zwischen ganzen und halben Verlierern: | ||
| Zeile 355: | Zeile 348: | ||
Hier erfolgt die Ansage bei Legen der ersten eigenen Karte (Ausnahme Anfragen). | Hier erfolgt die Ansage bei Legen der ersten eigenen Karte (Ausnahme Anfragen). | ||
| + | |||
Der Nachteil durch den mit der vorzeitigen Ansage verbundenen Informationsverzicht wird überkompensiert durch die Tatsache, daß der Partner nunmehr auch mit schwächeren Blättern eine | Der Nachteil durch den mit der vorzeitigen Ansage verbundenen Informationsverzicht wird überkompensiert durch die Tatsache, daß der Partner nunmehr auch mit schwächeren Blättern eine | ||
weiterführende Ansage treffen kann. Vor allen Dingen kann der Partner bisher unbedeutende | weiterführende Ansage treffen kann. Vor allen Dingen kann der Partner bisher unbedeutende | ||
| − | Trumpfkarten wie rote Damen oder eine | + | Trumpfkarten wie rote Damen oder eine [[Datei:KlpD.gif]] aufwerten. Auf eine KONTRA-Ansage bei Legen der ersten Karte wird häufig verzichtet. |
| − | ersten Karte wird häufig verzichtet. Dies geschieht aus zwei Gründen: | + | |
| + | Dies geschieht aus zwei Gründen: | ||
* Die Wahrscheinlichkeit, daß der Partner ein Blatt hält welches die keine 90-Ansage ermöglicht, | * Die Wahrscheinlichkeit, daß der Partner ein Blatt hält welches die keine 90-Ansage ermöglicht, | ||
ist geringer als bei dem RE-Partner. | ist geringer als bei dem RE-Partner. | ||
* Die Wahrscheinlichkeit, daß ein Spieler der Gegenpartei eine knappe Ansage auf der Hand | * Die Wahrscheinlichkeit, daß ein Spieler der Gegenpartei eine knappe Ansage auf der Hand | ||
hält, ist höher als bei einem starken RE-Spieler. In einigen Fällen wird nachträglich ein starkes | hält, ist höher als bei einem starken RE-Spieler. In einigen Fällen wird nachträglich ein starkes | ||
| − | KONTRA-Blatt deklariert. So kann z.B. bei eigenem Anspiel von klein Trumpf (Blatt: | + | KONTRA-Blatt deklariert. So kann z.B. bei eigenem Anspiel von klein Trumpf (Blatt: [[Datei:Klh10.gif]] [[Datei:KlpD.gif]][[Datei:KlhD.gif]][[Datei:KlhD.gif]] [[Datei:KlkB.gif]][[Datei:KlpB.gif]][[Datei:KlcB.gif]][[Datei:KlcB.gif]] [[Datei:KlcA.gif]][[Datei:KlcK.gif]] [[Datei:KlpK.gif]][[Datei:Klh9.gif]]), wobei an beliebiger Position eine [[Datei:Klh10.gif]] ohne |
| − | + | Ansage fällt, nun als Kommentar zur [[Datei:Klh10.gif]] KONTRA angesagt werden, da nun eine Ansage | |
| − | Ansage fällt, nun als Kommentar zur | ||
eines anderen Spielers sehr unwahrscheinlich ist. | eines anderen Spielers sehr unwahrscheinlich ist. | ||
| + | |||
| + | (...) Beispiele fehlen | ||
| + | |||
| + | Neben den bisher beschriebenen Ansagezeitpunkten sieht das Essener System noch eine [[RE-Ansage vor Anspiel]] der ersten Karte vor. Der Spieler zeigt damit, daß er definitiv angespielt werden kann. Hierzu muß er [[Datei:Klh10.gif]][[Datei:Klh10.gif]] (an Position 2 auch eine [[Datei:Klh10.gif]]) besitzen. Die Ansage charakterisiert ein starkes RE-Blatt. Es muß nicht unbedingt Asse enthalten. Der anspielende Partner ist nicht verpflichtet Trumpf anzuspielen. Spielt er ein As an, so zeigt er seine eigene Stärke analog dem vorherigen Beispiel durch die Wahl des Ansagezeitpunktes (mit Anspiel= sehr stark; vor Legen der Karte des starken Spielers = Blatt mit Zusatzwerten; keine Ansage = schwach). Das angespielte As sollte allerdings eine [[Lauf von Fehlkarten|Laufwahrscheinlichkeit]] von mindestens 66% (siehe Anhang Tab. A3) besitzen. | ||
| + | |||
| + | Die gleiche Ansage wird als KONTRA-Spieler nicht angewandt,da das Signalisieren der [[Datei:Klh10.gif]][[Datei:Klh10.gif]] eher für die RE-Partei nützlich ist. Sie wissen, daß der Partner des starken KONTRA-Spielers keine Kontrolle in Trumpf besitzt, was bei dem Partner eines starken RE-Spieler nicht der Fall wäre. | ||
=== 90-Anfragen === | === 90-Anfragen === | ||
| Zeile 379: | Zeile 379: | ||
Echte Vorteile sind zum Beispiel: | Echte Vorteile sind zum Beispiel: | ||
| − | * Abwurf eines Fehlverlierers in einer anderen als der angespielten Farbe | + | * Abwurf eines Fehlverlierers in einer anderen als der angespielten Farbe (Abwurf sollte [[Single|Singleton]] sein). |
| − | (Abwurf sollte [[Singleton]] sein). | ||
* Schmieren eines Fehlvollen in der angespielten Farbe (z. B. bei 10, 9). | * Schmieren eines Fehlvollen in der angespielten Farbe (z. B. bei 10, 9). | ||
| − | * Bedienen mit erkennbaren Singleton | + | * Bedienen mit erkennbaren Singleton (K oder 9, meist an Position 4, fordert das Nachspiel der Farbe). |
| − | (K oder 9, meist an Position 4, fordert das Nachspiel der Farbe). | ||
* Verhindern der Verschwendung eines hohen Trumpfes (an Position 3, wenn zwei kleine Trumpf liegen). | * Verhindern der Verschwendung eines hohen Trumpfes (an Position 3, wenn zwei kleine Trumpf liegen). | ||
| Zeile 1.061: | Zeile 1.059: | ||
von praktischem Nutzen. Wie wichtig eine einwandfreie Konvention für dieses | von praktischem Nutzen. Wie wichtig eine einwandfreie Konvention für dieses | ||
Gegenspielproblem ist zeigt das folgende Beispiel: (...) | Gegenspielproblem ist zeigt das folgende Beispiel: (...) | ||
| + | |||
| + | |||
| + | Bei der As-Signal-Konvention gelten folgende Regeln für die freiwilligen Abwürfe: | ||
| + | |||
| + | * Es werden möglichst eindeutig so viele Asse wie möglich mit Ausnahme von Doppelassen gezeigt. | ||
| + | * Der Abwurf einer Karte signalisiert: Wahrscheinlich ein As in der Farbe des Abwurfes. | ||
| + | * Ein Farbwechsel bestätigt das Vorhandensein des Asses, der zuvor gelegten Farbe. | ||
| + | * Es wird kein Voller Singleton gestellt, es sei denn der Spieler hält mehr als 4 Volle oder beide Asse sind bei der KONTRA-Partei. | ||
| + | * Asse, die aufgrund von Regel 3 nicht gezeigt werden können (z.B. bei As x oder As 10 x)werden durch ein Hoch-Niedrig-Signal bei Abwurf einer anderen Farbe gezeigt. Ein Hoch-Niedrig-Signal kann dabei durch eine Karte einer anderen Farbe unterbrochen werden. | ||
| + | * Die Signalfolge ist beendet, wenn eine Farbe wiederholt wird, oder wenn nach einem Hoch- | ||
| + | * Niedrig-Signal die Farbe gewechselt wird. | ||
| + | |||
| + | (...) | ||
==== Ansageverhalten der Gegenspieler ==== | ==== Ansageverhalten der Gegenspieler ==== | ||
| Zeile 1.227: | Zeile 1.238: | ||
= Ausflug in die Wahrscheinlichkeitsrechnung = | = Ausflug in die Wahrscheinlichkeitsrechnung = | ||
| + | |||
| + | ==Einleitung== | ||
| + | |||
| + | Ein Doppelkopfspieler muß schon nach dem Aufnehmen der Karten eine Entscheidung treffen. Er fragt sich, ob er mit seinem Blatt ein Solo spielen will oder ein Normalspiel vorzieht. Während des Spieles muß er entscheiden, welche Ansagen er treffen will. Je öfter er sich richtig entscheidet, desto mehr Punkte kann er auf seinem Konto verbuchen. Wenn man im Normalspiel tiefe Ansagen treffen will, sollte man wissen, mit welchen Trumpfverteilungen man rechnen muß. Will man einen As-Soli spielen, so sollte man wissen, wie zuversichtlich man sein kann, daß die lange Farbe durchzieht (Standard-As-Soli) und wenn man bei einem Buben-Solo vermutlich mehrfach vom Stich gehen muß, um eine Farbe zu entwickeln, so sollte man wissen, ob man damit rechnen muß, daß man wegen eines schlechten Sitzes der Buben gar nicht dazu kommt, die Farbe zu entwickeln. | ||
| + | |||
| + | Sind die kritischen Karten in diesen Beispielen günstig verteilt, so gewinnt man i.d.R. das Spiel, sonst verliert man. | ||
| + | |||
| + | Um die richtigen Entscheidungen treffen zu können, muß man also eine Vorstellung darüber haben, welche Verteilungen möglich sind und wie häufig diese jeweils vorkommen. Die Wahrscheinlichkeitsrechnung bietet nun die Möglichkeit die Häufigkeiten der verschiedenen kritischen Verteilungen vorauszusagen. Wenn man seine Entscheidung von diesen Verteilungswahrscheinlichkeiten | ||
| + | abhängig macht, wird man auf Dauer mehr Punkte sammeln, als wenn man diese Entscheidungen aus dem Bauch heraus trifft, da die Intuition täuschen kann. Das Spiel mit der Wahrscheinlichkeit verspricht allerdings nur Gewinne auf lange Sicht. Im Einzelfall können | ||
| + | bestimmte Karten durchaus völlig falsch sitzen, auch wenn dies extrem unwahrscheinlich ist. | ||
| + | |||
| + | Als Maß für den Wert eines Blattes dient der Erwartungswert, des Blattes. Dies ist die durchschnittliche Punktzahl, die man mit seinem Blatt in Abhängigkeit von den verschiedenen Verteilungen erzielt. Das Ziel ist es, diejenige Spielweise zu wählen, bei der der Erwartungswert möglichst groß ist. Bei Normalspielen ist der Erwartungswert häufig schwer zu berechnen, da er dort oft von einer Vielzahl von Faktoren abhängt. Beim Solo ist die Berechnung meistens erheblich leichter durchzuführen, da hier nur ein oder zwei Faktoren wichtig sind. Daher wird sich dieses Kapitel auch zu einem großen Teil mit den Fragestellungen aus dem Solo beschäftigen. | ||
| + | |||
| + | ==Grundbegriffe der Wahrscheinlichkeitsrechnung== | ||
| + | |||
| + | Die Wahrscheinlichkeitsrechnung befaßt sich mit den Vorgängen, deren Ausgang nicht vorhersagbar ist. Dies kann daran liegen, daß man gewisse Bedingungen, unter denen ein solcher Vorgang stattfindet, nicht kennt oder daran, daß der Vorgang selbst nicht vollständig durchschaut wird. Wirft man beispielsweise eine Münze in die Luft, so kann nicht vorhergesagt werden, ob Kopf oder Zahl nach oben zeigen wird. Um dies vorauszuberechnen müßte man umfangreiche Daten über den Münzwurf zusammentragen (Stärke des Wurfes, Anfangsrotation der Münze, Materialverteilung in der Münze und damit das Rotationsverhalten der Münze, Luftdruck etc.). | ||
| + | |||
| + | Wiederholt man den Münzwurf sehr oft, wird man feststellen, daß jede Seite in etwa der Hälfte der Fälle nach oben zeigt (wenn es sich nicht gerade um eine deformierte Münze handelt). Die einander ausschließenden möglichen Ausgänge eines Versuches heißen Elementarereignisse. Der Münzwurf hat zwei Elementarereignisse: 1) "Kopf weist nach oben" und 2) "Zahl weist nach | ||
| + | oben". Beim Werfen eines Würfels gibt es sechs einander ausschließende Elementarereignisse. | ||
| + | |||
| + | Jeder mögliche Ausgang eines Versuches wird Ereignis genannt. Ein Ereignis kann aus mehreren Elementarereignissen zusammengesetzt sein. So ist das Ereignis "man würfelt eine gerade Zahl" aus den Elementarereignissen "man würfelt eine zwei", "man würfelt eine vier" und "man würfelt eine sechs" zusammengesetzt. Zwei Ereignisse heißen unvereinbar, wenn sie nicht gleichzeitig eintreten können. Man kann z.B. mit einem Würfel nicht gleichzeitig eine vier und eine ungerade Zahl würfeln. Zwei Ereignisse heißen unabhängig, wenn das Eintreten des einen Ereignisses keinen Einfluß auf das Eintreten des anderen Ereignisses hat. Würfelt man zweimal hintereinander, so beeinflußt der erste Wurf sicherlich nicht den Ausgang des zweiten Wurfes. | ||
| + | |||
| + | Kommen wir nun zur klassischen Definition der Wahrscheinlichkeit (dies setzt voraus, daß es endlich viele Elementarereignisse gibt, die alle gleichmöglich sind). Die Wahrscheinlichkeit, daß | ||
| + | ein Ereignis A eintritt wird definiert als: | ||
| + | |||
| + | p(A) =Anzahl aller möglichen Elementarereignisse / Anzahl der für A günstigen Elementarereignisse | ||
| + | |||
| + | Die Wahrscheinlichkeit eine drei zu würfeln ist also 1/6. Die Wahrscheinlichkeit eine gerade Zahl zu würfeln ist 3/6 = 1/2. Das sichere Ereignis "man würfelt eine Zahl von eins bis sechs" hat die Wahrscheinlichkeit 6/6 = 1. Das unmögliche Ereignis "man würfelt eine sieben" hat die Wahrscheinlichkeit 0/6 = 0. Wahrscheinlichkeiten werden also durch Zahlen zwischen 0 und 1 repräsentiert. | ||
| + | Häufig werden sie jedoch als Prozentzahlen dargestellt, indem sie einfach mit 100 multipliziert (und mit einem Prozentzeichen versehen) werden. Das sichere Ereignis hat dann die Wahrscheinlichkeit von 100% und das unmögliche Ereignis hat die Wahrscheinlichkeit 0%. | ||
| + | |||
| + | Man steht häufig vor der Frage, wie wahrscheinlich ist es, daß entweder ein Ereignis A oder ein | ||
| + | Ereignis B eintritt. Sind diese Ereignisse A und B unvereinbar, so kann die gesuchte Wahrscheinlichkeit | ||
| + | leicht berechnet werden, denn es gilt: | ||
| + | |||
| + | Man steht häufig vor der Frage, wie wahrscheinlich ist es, daß entweder ein Ereignis A oder ein | ||
| + | Ereignis B eintritt. Sind diese Ereignisse A und B unvereinbar, so kann die gesuchte Wahrscheinlichkeit | ||
| + | leicht berechnet werden, denn es gilt: | ||
| + | |||
| + | '''Regel 1:''' | ||
| + | Die Wahrscheinlichkeit, daß von zwei unvereinbaren Ereignissen A und B wenigstens | ||
| + | eines eintritt, ist die Summe der beiden Einzelwahrscheinlichkeiten. | ||
| + | |||
| + | : p(A oder B) = p(A) + p(B) | ||
| + | |||
| + | Dies gilt analog auch für mehr als zwei unvereinbare Ereignisse. Ebenso häufig möchte man | ||
| + | wissen, wie wahrscheinlich es ist, daß sowohl Ereignis A als auch Ereignis B eintritt. Sind A und | ||
| + | B unabhängig voneinander, so gilt die | ||
| + | |||
| + | '''Regel 2:''' | ||
| + | Die Wahrscheinlichkeit, daß die voneinander unabhängigen Ereignisse A und B beide | ||
| + | eintreten, ist das Produkt der Einzelwahrscheinlichkeiten. | ||
| + | |||
| + | : p(A und B) = p(A) × p(B) | ||
| + | |||
| + | Auch dies kann man für mehrere Ereignisse verallgemeinern. Leider ist es häufig so, daß die | ||
| + | Ereignisse nicht unabhängig sind. Ganz allgemein gilt die | ||
| + | |||
| + | '''Regel 3:''' | ||
| + | Die Wahrscheinlichkeit, daß die Ereignisse A und B beide eintreten ist das Produkt der | ||
| + | Wahrscheinlichkeiten von A mit der Wahrscheinlichkeit von B unter der Voraussetzung, | ||
| + | daß A eingetreten ist. | ||
| + | |||
| + | : p(A und B) = p(A) × p(B, vorausgesetzt A ist eingetreten) | ||
| + | |||
| + | Ein Beispiel: | ||
| + | |||
| + | A sei das Ereignis "man würfelt eine Zahl kleiner als vier" und B das Ereignis "man würfelt eine ungerade Zahl" Hier kann man das Ergebnis auch ohne große Rechnung angeben, da offensichtlich nur die Elementarereignisse "man würfelt eine 1" und "man würfelt eine drei" günstig sind. Also ist die Wahrscheinlichkeit 2/6 = 1/3. Versuchen wir noch die Rechnung nach der Regel 3. Die Wahrscheinlichkeit für das Würfeln einer Zahl kleiner vier ist 3/6 = 1/2. Die Wahrscheinlichkeit eine ungerade Zahl zu würfeln unter Voraussetzung Ereignis A ist eingetreten offensichtlich 2/3. Dann ergibt sich nach Regel 3 mit p(A und B) = 1 2 × 2 3 = 1 3 das erwartete Ergebnis. Die Regel 2 ist ein Sonderfall der Regel 3 für unabhängige Ereignisse. | ||
| + | |||
| + | Bei den meisten Berechnungen reicht es aus so zu tun, als ob die Ereignisse unabhängig wären, da der entstehende Fehler ziemlich klein ist, während der gesparte Arbeitsaufwand meist recht groß ist. Spielt man z.B. als Hochzeiter zum ersten Stich sein blankes [[Datei:KlhA.gif]] und es fallen [[Datei:Klh9.gif]] [[Datei:KlcA.gif]] [[Datei:KlcB.gif]], so weiß man, daß die restlichen [[Datei:Herz.gif]] 4-0-0 verteilt sind. | ||
| + | |||
| + | Berechnet man nun, wie wahrscheinlich es ist, daß jeder Spieler mindestens ein [[Datei:Pik.gif]] hält, wenn man selbst [[Datei:KlpA.gif]][[Datei:KlpA.gif]][[Datei:Klp9.gif]] hat, so beträgt sie 64,2%. Wäre das [[Datei:KlhA.gif]] nichtssagend gelaufen, wären es 67,3%. Der Rechenaufwand für die erste Zahl ist erheblich größer (wer will kann es ja nachprüfen), doch der Fehler ist nicht besonders groß, obwohl schon eine ziemlich extreme Verteilung vorliegt. Braucht man also keine genauen, sondern reichen ungefähre Zahlen, lohnt sich der Aufwand nicht. | ||
| + | |||
| + | Will man schließlich wissen, wann von zwei Ereignissen, die miteinander vereinbar sind, wenigstens | ||
| + | eines eintritt, muß man die Regel 1 abändern. Es gilt allgemein die | ||
| + | |||
| + | Regel 4: | ||
| + | Die Wahrscheinlichkeit, daß von zwei Ereignissen A und B wenigstens eines eintritt, | ||
| + | ist die Summe der beiden Einzelwahrscheinlichkeiten verringert um die | ||
| + | Wahrscheinlichkeit, daß beide Ereignisse eintreten. | ||
| + | |||
| + | :p(A oder B) = p(A) + p(B) - p(A und B) | ||
| + | |||
| + | Die Regel 1 wird damit zum Sonderfall der Regel 4, wenn p(A und B) = 0 ist, was genau dann der | ||
| + | Fall ist, wenn A und B unvereinbar sind. | ||
| + | |||
| + | ==Die Hypergeometrische Verteilung== | ||
(...) | (...) | ||
| + | === Tab. A1:Verteilungswahrscheinlichkeiten === | ||
| + | |||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |- | ||
| + | | [[bild:Essener_System-71.gif|thumb|Teil 1|100px]] || [[bild:Essener_System-72.gif|thumb|Teil 2|100px]]||[[bild:Essener_System-73.gif|thumb|Teil 3|100px]] | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | Die Wahrscheinlichkeiten für n = 11 (also in Kenntnis des ersten Stiches) gelten streng genommen nur, wenn im ersten Stich alle Spieler bedient haben mit den interessanten Karten und die interessanten Karten alle keinen besonderen Informationsgehalt bezüglich der Verteilung der restlichen Karten besitzen. Für den Fall, daß eine besondere Karte (woraus folgt: Der Spieler besitzt keine weitere der kritischen Karten) gefallen ist oder ein Spieler nicht bedient hat, kann die Tabelle A2 herangezogen werden. | ||
| + | |||
| + | === Tab. A2:Verteilungswahrscheinlichkeiten === | ||
| + | |||
| + | [[bild:Essener_System-73.gif|thumb|A2|100px]] | ||
| + | |||
| + | Diese beiden Tabellen (auf Formel 2 basierend) sind die Grundlage für alle weiteren Berechnungen. Mit ihrer Hilfe und den Regeln 1-3 der Wahrscheinlichkeitsrechnung ist es möglich eine Vielzahl für den Doppelkopfspieler relevanten Wahrscheinlichkeiten näherungsweise zu berechnen. Strenggenommen darf man nicht mit den Verteilungswahrscheinlichkeiten aus Tabelle A1 arbeiten, | ||
| + | da schon durch die Vorbehaltsabfrage Informationen über den Spielverlauf gegeben werden, die die Wahrscheinlichkeiten verändern. Genauer müßten mit Formel 3 die Wahrscheinlichkeiten neu berechnet werden, wobei allein schon zwischen RE-Spieler und KONTRA-Spieler | ||
| + | unterschieden werden müßte (durch den Besitz, bzw. Nichtbesitz von §D hat der Spieler entweder schon eine bestimmte Karte bzw. ihm stehen bei der Austeilung definitiv nur 46 Karten zur Verfügung). Doch hier gilt , daß in den meisten Fällen die Abweichung klein ist, während der zusätzliche Aufwand groß ist. Die Verteilungswahrscheinlichkeiten aus Tabelle A1 sind für Spieler mit mindestens einer [[Datei:KlkD.gif]] und für Solospieler links vom Geber, die ihr Solo taufen bevor die anderen Spieler einen Vorbehalt melden konnten, korrekt, da hier die Vorbehaltsabfrage keinerlei Informationen enthält. | ||
| + | |||
| + | == Berechnung nützlicher Wahrscheinlichkeiten == | ||
| + | |||
| + | Es folgen nun einige Beispiele für die Anwendung der Tabellen A1 und A2 zur Berechnung von Wahrscheinlichkeiten. Bei der Berechnung wird - wenn nicht ausdrücklich etwas anderen angegeben wird - immer von der Situation unmittelbar vor Spielbeginn ausgegangen. Einige wichtige Wahrscheinlichkeiten für den täglichen Gebrauch sind dann in den Tabellen A3 bis A7 dargestellt. | ||
| + | |||
| + | === Beispiel 1 === | ||
| + | Spieler hält 9 Trumpf und [[Datei:KlpA.gif]][[Datei:Klp9.gif]] [[Datei:KlcK.gif]] als Fehlkarten | ||
| + | |||
| + | Wie wahrscheinlich ist es nun , daß | ||
| + | # kein Mitspieler gleich viele Trumpf als er selbst hält, | ||
| + | # das [[Datei:KlpA.gif]] läuft und | ||
| + | # er beide [[Datei:Kreuz.gif]]-Runden alleine sticht. | ||
| + | |||
| + | ==== Beispiel 1 zu 1. ==== | ||
| + | |||
| + | Es fehlen 26 - 9 = 17 Trumpf = interessante Karten. | ||
| + | |||
| + | Die günstigen Verteilungen sind: | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+ Die günstigen Verteilungen sind: | ||
| + | ! Verteilungen !! Wahrscheinlichkeiten | ||
| + | |- | ||
| + | | 6-6-5 || 23,59% | ||
| + | |- | ||
| + | | 7-5-5 || 17,34% | ||
| + | |- | ||
| + | | 7-6-4 || 25,28% | ||
| + | |- | ||
| + | | 7-7-3 || 4,82% | ||
| + | |- | ||
| + | | 8-5-4 || 13,54% | ||
| + | |- | ||
| + | | 8-6-3 || 7,02% | ||
| + | |- | ||
| + | | 8-7-2 || 1,81% | ||
| + | |- | ||
| + | | 8-8-1 || 0,10% | ||
| + | |- | ||
| + | |Summe:||93,50% | ||
| + | |} | ||
| + | |||
| + | (siehe Tab. A1 für M = 17). | ||
| + | |||
| + | '''In ungefähr 9 von 10 Fällen besitzt ein Spieler mit 9 Trumpf die absolute Trumpfüberlegenheit'''. Nehmen wir nun zusätzlich | ||
| + | den Fall an, daß zum ersten Stich Trumpf angespielt wird und alle Spieler bedienen, so kann die Wahrscheinlichkeit neu berechnet werden: | ||
| + | |||
| + | Es fehlen nun 26 - 9 - 3 = 14 | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+ Die günstigen Verteilungen sind: | ||
| + | ! Verteilungen !! Wahrscheinlichkeiten | ||
| + | |- | ||
| + | | 5-5-4 || 23,59% | ||
| + | |- | ||
| + | | 6-4-4 || 18,43% | ||
| + | |- | ||
| + | | 6-5-3, || 25,81% | ||
| + | |- | ||
| + | | 6-6-2 ||4,30% | ||
| + | |- | ||
| + | | 7-4-3 || 13,17% | ||
| + | |- | ||
| + | | 7-5-2 || 6,14% | ||
| + | |- | ||
| + | | 7-6-1 || 1,23% | ||
| + | |- | ||
| + | | 7-7-0 || 0,04% | ||
| + | |- | ||
| + | |Summe:||94,93% | ||
| + | |} | ||
| + | |||
| + | (siehe Tab. A1 für M = 14 und n = 11). | ||
| + | |||
| + | ==== Beispiel 1 zu 2. ==== | ||
| + | |||
| + | Es fehlen bei [[Datei:KlpA.gif]][[Datei:Klp9.gif]] genau 6 interessante Karten. Die günstigen Verteilungen sind alle diejenigen, in denen keiner der übrigen drei Spieler eine [[Chicane]] besitzt. | ||
| + | |||
| + | Dies sind: | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+ Die günstigen Verteilungen sind: | ||
| + | ! Verteilungen !! Wahrscheinlichkeiten | ||
| + | |- | ||
| + | | 2-2-2 || 14,76% | ||
| + | |- | ||
| + | | 3-2-1 || 53,67% | ||
| + | |- | ||
| + | | 4-1-1, || 10,98 | ||
| + | |- | ||
| + | |Summe:||79,41% | ||
| + | |} | ||
| + | |||
| + | Bei einer Ansage kommt noch die Fälle hinzu, daß nur der Partner Chicane in der Farbe ist. Der Einfachheit halber nehmen wir an, daß von den Verteilungen, bei denen genau ein Spieler Chicane ist, ein Drittel günstig ist. In Wirklichkeit ist der Anteil für Re-Spieler etwas größer als für einen KONTRA-Spieler. | ||
| + | |||
| + | Wir berücksichtigen noch die Verteilungen: | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+ Chicane beim Mitspieler | ||
| + | ! Verteilungen !! Wahrscheinlichkeiten | ||
| + | |- | ||
| + | | 5-1-0 || 2,93% | ||
| + | |- | ||
| + | | 4-2-0 || 10,06% | ||
| + | |- | ||
| + | | 3-3-0, || 7,45% | ||
| + | |- | ||
| + | |Günsteige||79,41% | ||
| + | |- | ||
| + | |Summe:||86,22% | ||
| + | |} | ||
| + | |||
| + | Weitere Angaben zu diesem Thema siehe Tab. A3. | ||
| + | |||
| + | ==== Beispiel 1 zu 3. ==== | ||
| + | |||
| + | Es fehlen insgesamt 8 interessante Karten. | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+ Die günstigen Verteilungen sind: | ||
| + | ! Verteilungen !! Wahrscheinlichkeiten | ||
| + | |- | ||
| + | | 3-3-2 || 31,67% | ||
| + | |- | ||
| + | | 4-2-2 || 21,38% | ||
| + | |- | ||
| + | |Summe:||53,05% | ||
| + | |} | ||
| + | |||
| + | Bei einer Ansage erhöht sich Wahrscheinlichkeit analog wie bei dem vorherigen Beispiel, da nun ursprünglich ungünstige Verteilungen teilweise miteinbezogen werden können. | ||
| + | |||
| + | Weitere Werte (mit Ansage d.h. Partner kann mitstechen, Spieler hält keine Chicane sondern Singleton, [[Datei:KlhA.gif]]-Stechen) befinden sich in Tab. A4. | ||
| + | |||
| + | (...) weitere Beispiel fehlen | ||
| + | |||
| + | == Tab. A3: Laufwahrscheinlichkeit von Assen im Normalspiel == | ||
| + | |||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+. | ||
| + | ! fehlende Karten in der kritischen Farbe !! 7 !! 6 !! 5 !! 4 !! 3 | ||
| + | |- | ||
| + | |Laufwahrscheinlichkeit '''ohne''' Ansage ||87,6%|| 79,4%|| 66,8%|| 48,4%|| 24,2% | ||
| + | |- | ||
| + | |Laufwahrscheinlichkeit '''mit''' Ansage ||91,7%|| 86,2%|| 77,7%|| 64,8%|| 46,4% | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | == Tab. A4: Wahrscheinlichkeit eine Fehlfarbe allein zu stechen im Normalspiel == | ||
| + | |||
| + | |||
| + | {| style=" background: #c0c0c0; margin-right: 1em; border-spacing: 1px;" | ||
| + | |- align="center" | ||
| + | | style="background: #d8d8d8;" colspan="1" | . | ||
| + | | style="background: #d8d8d8;" colspan="2" | zweimaliges Stechen bei '''Chicane''' | ||
| + | | style="background: #d8d8d8;" colspan="2" | einmaliges Stechen bei '''Singleton''' | ||
| + | |- align="center" | ||
| + | | style="background: #e3e3e3;" | | ||
| + | | style="background: #e3e3e3;" | [[Datei:Pik.gif]]/[[Datei:KlkA.gif]] | ||
| + | | style="background: #e3e3e3;" | [[Datei:Herz.gif]] | ||
| + | | style="background: #e3e3e3;" | [[Datei:Pik.gif]]/[[Datei:KlkA.gif]] | ||
| + | | style="background: #e3e3e3;" | [[Datei:Herz.gif]] | ||
| + | |- | ||
| + | | style="background: #ffffff;" | Laufwahrscheinlichkeit '''ohne''' Ansage | ||
| + | | style="background: #ffffff;" | 53,1% | ||
| + | | style="background: #ffffff;" | 14,8% | ||
| + | | style="background: #ffffff;" | 34,4% | ||
| + | |- | ||
| + | | style="background: #ffffff;" | Laufwahrscheinlichkeit '''mit''' Ansage | ||
| + | | style="background: #ffffff;" | 68,2% | ||
| + | | style="background: #ffffff;" | 38,5% | ||
| + | | style="background: #ffffff;" | 54,7% | ||
| + | | style="background: #ffffff;" | 21,6% | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | == Tab. A5: Wahrscheinlichkeit ein blankes As zu fangen == | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+. | ||
| + | ! fehlende Karten in der kritischen Farbe !! 6 !! 5 !! 4 !! 3 !! 2 | ||
| + | |- | ||
| + | |Wahrscheinlichkeit, daß As zu fangen ||13,1% ||20,3%|| 30,9% ||46,4% ||68,6% | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | == Tab. A6: Wahrscheinlichkeit alle Buben/Damen beim Buben/Damen-Solo zu fangen == | ||
| + | |||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+. | ||
| + | ! eigene Trümpfe !! Wahrscheinlichkeit !! eigene Trümpfe !! Wahrscheinlichkeit | ||
| + | |- | ||
| + | |[[Datei:Kreuz.gif]], [[Datei:Kreuz.gif]], [[Datei:Pik.gif]] ||89,9%|| [[Datei:Kreuz.gif]], [[Datei:Pik.gif]], [[Datei:Pik.gif]]|| 18,4% | ||
| + | |- | ||
| + | |[[Datei:Kreuz.gif]], [[Datei:Kreuz.gif]], [[Datei:Herz.gif]] ||46,4% ||[[Datei:Kreuz.gif]], [[Datei:Pik.gif]], [[Datei:Herz.gif]] ||10,8% | ||
| + | |- | ||
| + | |[[Datei:Kreuz.gif]], [[Datei:Kreuz.gif]], [[Datei:KlcB.gif]]|| 41,6% ||[[Datei:Kreuz.gif]], [[Datei:Pik.gif]], [[Datei:KlcB.gif]] ||8,3% | ||
| + | |- | ||
| + | |[[Datei:Kreuz.gif]], [[Datei:Kreuz.gif]], [[Datei:Pik.gif]], x|| 97,8%|| [[Datei:Kreuz.gif]], [[Datei:Pik.gif]], [[Datei:Pik.gif]], x ||30,9% | ||
| + | |- | ||
| + | |[[Datei:Kreuz.gif]], [[Datei:Kreuz.gif]], x, x ||70,6%|| [[Datei:Kreuz.gif]], [[Datei:Pik.gif]], x, x ||24,2% | ||
| + | |- | ||
| + | |[[Datei:Kreuz.gif]], [[Datei:Kreuz.gif]], x, x, x ||90,8%|| [[Datei:Kreuz.gif]], [[Datei:Herz.gif]], x, x, x ||24,2% | ||
| + | |- | ||
| + | |[[Datei:Kreuz.gif]], [[Datei:Pik.gif]], x, x, x ||46,4% ||[[Datei:Kreuz.gif]], x, x, x, x, x ||68,6% | ||
| + | |} | ||
| + | |||
| + | x = beliebige(r) andere(r) rote(r) ([[Datei:Herz.gif]]/[[Datei:Karo.gif]])eigen(r) Bube/Dame | ||
| + | |||
| + | == Tab. A7: Wahrscheinlichkeit keinen Verlierer mit doppel AS zu besitzen == | ||
| + | |||
| + | Wahrscheinlichkeit mit einer langen Farbe mit As As x (=K) an der Spitze keinen Verlierer zu besitzen | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |+ | ||
| + | ! Struktur der Farbe !! n = 12 !!Struktur der Farbe !! n = 12 | ||
| + | |- | ||
| + | | As, As, x, x, x, x ||14,8% ||As, As, K, x, x|| 9,8% | ||
| + | |- | ||
| + | | As, As, x, x, x, x, x ||41,6%|| As, As, K, x, x, x ||25,5% | ||
| + | |- | ||
| + | |As, As, x, x, x, x, x, x ||70,6%|| As, As, K, x, x, x, x ||46,4% | ||
| + | |- | ||
| + | |As, As, x, x, x, x, x, x, x ||90,8%|| As, As, K, x, x, x, x, x ||70,6% | ||
| + | |} | ||
| + | |||
| + | x = beliebige andere eigene Karte in der Farbe | ||
| + | |||
| + | == Tab A8: fehlt(!) == | ||
[[Category:DokoLexikon]] | [[Category:DokoLexikon]] | ||
Aktuelle Version vom 13. August 2010, 13:30 Uhr
Quelle siehe: http://de.wikipedia.org/wiki/Essener_System
Weblink: http://mwolff.info/Essener_System.pdf
Die hier dargestellten Textpassagen sind Auszüge aus den oben genannten Original... gekürzte Stellen werden durch (...) angezeigt...
Vielleicht findet sich noch jemand der die Beispiele und Tabellen einbauen kann...
Vorwort
Liebe Doppelkopffreunde!
Jeder von Euch kennt zumindest dem Namen nach noch eine ganze Reihe weitere Kartenspiele, wie zum Beispiel Bridge, Skat, Uno, Romme, Mau-Mau, Poker u.v.a.. Warum hat ausgerechnet Doppelkopf in Euch und uns so begeisterte Anhänger gefunden? Die Gründe liegen sicherlich darin, daß Doppelkopf zu den spieltechnisch und strategisch anspruchsvollsten Kartenspielen zu zählen ist und, daß Doppelkopf ein Partnerspiel ist.
Das Spielziel beim Turnierdoppelkopf besteht darin, zusammen mit verschiedenen Partnern so viele Spiele so hoch wie möglich zu gewinnen. Mitentscheidend hierfür ist in jedem Spiel das Verständnis mit dem jeweiligen Spielpartner. Je mehr Informationen hinsichtlich der Stärke und Struktur der Blätter man austauschen kann, desto leichter fällt es einen optimalen Spielplan für die eigene Partei zu finden und somit ein Maximum an Spielpunkten zu sammeln. Hierbei müssen selbstverständlich die Spielregeln und die Regeln des Fair Play eingehalten werden. Aktionen wie zum Beispiel "Wenn ich mit links ausspiele bin ich KONTRA-Spieler und wenn ich mit rechts ausspiele bin ich RE-Spieler" oder nicht regelgerechte Aussprüche wie zum Beispiel "Hallo Partner, ich mach den Stich" sind selbstverständlich zu verurteilen. Trotzdem ist es möglich regelgerecht detaillierte Informationen auszutauschen. Beispiele hierzu hat Bernhard Kopp in seinem Buch "Gewinnen beim Doppelkopf" gegeben. Wir erinneren nur an die Bedeutungen von Ansagezeitpunkten, 90-Anfragen und einigen Konventionen (As-Signal, Farbvorzugsignal bei As-Soli oder Hoch-Niedrig-Markierungen bei Normalspielen).
Warum also nun dieses Ausarbeitung? Hierfür gibt es mehrere Gründe: Das Doppelkopfspiel hat in der Zwischenzeit eine rasante Weiterentwicklung erfahren. Inspiriert durch Berhard's Buch, ist das Doppelkopfspiel mit vielen neuen Ideen bereichert worden. Leider haben unsere persönlichen Erfahrungen gezeigt, daß diese neuen (und auch einige alte) Ideen zur Informationsübermittlung nur wenigen Insidern bekannt sind bzw. nur von wenigen Doppelkopffreunden in ihrer Gesamtheit verstanden und korrekt angewendet werden. Ein prägnantes Beispiel in diesem Zusammenhang ist sicherlich die Dullenkonvention (Vorspiel der ![]() bis zum dritten Stich). Zudem fehlt es an einem logischen Gesamtkonzept für die regelgerechte Kommunikation zwischen den Spielpartnern.
bis zum dritten Stich). Zudem fehlt es an einem logischen Gesamtkonzept für die regelgerechte Kommunikation zwischen den Spielpartnern.
In dieser Ausarbeitung stellen wir daher ein umfangreiches, auf Logik aufbauendes Kommunikationssystem vor, daß sich zum größten Teil in der Praxis bereits hervorragend bewährt hat und zu einem kleinen Teil vollkommen neue Aspekte enthält, die in der Praxis noch erprobt werden müssen. Wir haben es aufgrund unserer Vereinszugehörigkeit zur "Geknickten Dulle Essen 88 e.V." kurz das "Essener System" genannt. Im wesentlichen beantworten wir folgende Fragen:
- Wann bzw. unter welchen Bedingungen ist ein Austausch von Informationen überhaupt sinnvoll ?
- Welche regelgerechten "Hilfsmittel" stehen dem Doppelkopfspieler zur Informationsübermittlung zur Verfügung?
- Welche Regeln gelten für ihre Anwendung?
- Wie hängt die Interpretation des angewendeten Hilfsmittels von der speziellen Spielsituation ab?
Wir würden uns freuen, wenn Ihr uns nach einer kritischen Auseinandersetzung mit dieser Ausarbeitung Eure Beobachtungen hinsichtlich Mängel oder Verbesserungsvorschlägen zukommen laßt. Unser besonderer Dank gilt Ralf Schmidt (MG 1MDV) für seine Hinweise zur vorletzten Fassung und Michael Remme (E GD88) für das Layout des Titelblattes. Ferner danken wir allen Doppelkopffreunden, die uns in den letzten zwei Jahren direkt oder indirekt dazu ermuntert haben, unsere Spielweise schriftlich zu fixieren.
Viel Spaß beim Lesen und Nachspielen der angegebenen Beispiele wünschen Euch
Claus Günther, Jörg Passenberg und Heinz Zedler
(...)
Inhaltsverzeichnis
[Verbergen]- 1 Übersicht
- 2 Normalspiel
- 3 Hochzeit
- 4 Solo
- 5 Ausflug in die Wahrscheinlichkeitsrechnung
- 5.1 Einleitung
- 5.2 Grundbegriffe der Wahrscheinlichkeitsrechnung
- 5.3 Die Hypergeometrische Verteilung
- 5.4 Berechnung nützlicher Wahrscheinlichkeiten
- 5.5 Tab. A3: Laufwahrscheinlichkeit von Assen im Normalspiel
- 5.6 Tab. A4: Wahrscheinlichkeit eine Fehlfarbe allein zu stechen im Normalspiel
- 5.7 Tab. A5: Wahrscheinlichkeit ein blankes As zu fangen
- 5.8 Tab. A6: Wahrscheinlichkeit alle Buben/Damen beim Buben/Damen-Solo zu fangen
- 5.9 Tab. A7: Wahrscheinlichkeit keinen Verlierer mit doppel AS zu besitzen
- 5.10 Tab A8: fehlt(!)
Übersicht
Das Primärziel jedes erfolgsuchenden Dokospielers ist sicherlich aus den eigenen Karten und den Kartenverteilungen die optimale Punktausbeute zu erzielen. Ein Teilaspekt ist hierbei die optimale Ausreizung der Blätter der eigenen Partnerschaft. Hierbei vor allem soll das Essener System behilflich sein, indem es im wesentlichen die Sicherheit von Ansagen (inkl. Gegenansagen) erhöht. Dies geschieht dadurch, daß dem Ansagenden zum Zeitpunkt seiner Ansage, der ja i.d.R. recht früh (1-3. Stich) liegt, ein höherer Wissensstand über das Spiel (hinsichtlich Kartenverteilungen, Parteizugehörigkeit der Mitspieler, etc.) zu teil wird. Das Essener System zeigt Wege auf, wie man zum einen Informationen (hinsichtlich Struktur, Stärke seines Blattes, Parteizugehörigkeit, Besitz bestimmter Karten etc.) gibt und zum anderen erhalten kann. Dabei gelten folgende Grundprinzipien: Eine Information über das eigene Blatt wird dann freiwillig gegeben, wenn hierdurch der Erwartungswert für die eigene Partei erhöht wird. Dies ist i.d.R. dann der Fall, wenn man über ein überdurchschnittliches Blatt verfügt oder/und im Spiel gerade die Initiative im Spiel besitzt, da die Gegenpartei ja letztendlich genauso informiert wird.
Eine von einem Partner geforderte Information wird grundsätzlich gegeben.
Hier gibt es nur eine einzige Ausnahme:
Man besitzt weitere Informationen über das Spiel, die der Partner bei seinen Überlegungen unmöglich hat mit einbeziehen können. Das Essener System verwendet zur Informationsübermittlung die folgenden, selbstverständlich regelkonformen Hilfsmittel (zumeist Kombinationen):
- Ansagen (Verzicht auf eine Ansage).
- Wahl des Ansagezeitpunktes.
- Warten vor Legen bzw. Anspiel einer eigenen Karte (Simuliertes Überlegen).
- (Anspiel-)Konventionen.
Die einzelnen Komponenten haben dabei die folgenden Grundbedeutungen:
Ansagen
Ansagen werden im Essener System immer dann verwendet, wenn dadurch der Erwartungswert des Spiels, welcher repräsentiert wird durch die Summe der Wahrscheinlichkeiten aller möglichen Spielausgänge, jeweils mit dem zugehörigen Spielwert multipliziert, für die eigene Partei erhöht wird. Es muß also immer geprüft werden, welchen Einfluß eine Ansage auf den Spielverlauf haben kann. Die folgende Tabelle zeigt, welche Sicherheit rein mathematisch für die einzelnen Ansagen, bzw. welche Erhöhung der Erfolgsaussichten (bezieht sich auf Gegenansagen) notwendig sind, wenn man das bestehende Punktsystem als Grundlage verwendet.
Tab.1: Notwendige Sicherheiten bei (Gegen)-Ansagen
| Ansagen | Sicherheit für Ansagen | Wahrscheinlichkeitserhöhung für Gegenansagen |
|---|---|---|
| RE/KONTRA | >=50,00% | >=18,18% |
| keine 90 | >=88,89% | >=14,29% |
| keine 60 | >=91,67% | >=11,76% |
| keine 30 | >=93,33% | >=10,00% |
| Schwarz | >=94,74% | >=8,33% |
Die Angaben in der Tabelle gelten immer für den Fall, daß die vorherige eigene oder gegnerische (ohne die Gegenansage) Ansage eine Wahrscheinlichkeit von 100% besitzt. Weiterhin dienen Ansagen als (i.d.R. positive) Antworten auf Anfragen des Partners.
Wahl des Ansagezeitpunktes
Es gilt folgendes Grundprinzip:
Jeder Ansagezeitpunkt, der nicht mit dem letztmöglichen Zeitpunkt für die Ansage identisch ist, beinhaltet Zusatzinformationen. Diese Zusatzinformationen ergeben sich durch die Wahl des Ansagezeitpunktes häufig auch in Verbindung mit der Spielsituation. Wir unterscheiden folgende Ansagezeitpunkte:
Ansage bei Legen der eigenen Karte oder einer Karte eines Mitspielers
Dies bedeutet bei der Erstansage im Spiel generell besondere Stärke und kann zusätzlich auch das Vorhandensein oder Fehlen von bestimmten Karten signalisieren. Ausnahmen sind Ansagen als Antwort oder als Warnsignal bei Konventionssituationen. Ist die eigene Ansage nicht die erste der eigenen Partei, so ist sie i.d.R. ein Kommentar zur Karte oder Farbe (meist mit der Idee, dadurch den Besitz weiterer Karten zu signalisieren oder zu verneinen). Bei Gegenansagen können beide Interpretationen vorkommen.
Ansage vor dem Anspiel
Sie dient bei ungeklärter eigener Parteizugehörigkeit i.d.R. zur Partnerschaftsklärung (Man gibt sich dem Anspielenden, dem vermutlichen bzw. sicheren Partner zu erkennen). Ist die eigene Parteizugehörigkeit geklärt, so soll sie den Anspielenden (Partner) vom Normalanspiel abbringen. Was verstehen wir unter Normalanspiel? Es ist das Anspiel, welches in der jeweiligen Spielsituation (ohne die Ansage) das objektiv beste ist. Bei dieser Beurteilung darf der Anspielende sein eigendes Blatt, da der Ansagende es i.d.R. nicht exakt kennen kann, in seinen Überlegungen nicht mit einbeziehen.
Warten vor Legen bzw. Anspiel der eigenen Karte (Simuliertes Überlegen)
Dies ist immer eine Anfrage an den Partner nach bestimmten Informationen. Die geforderte Information im Einzelfall kann unterschiedlicher Natur sein: Bist du mein Partner; Partner machst du diesen Stich; Partner besitzt du eine bestimmte Karte; Partner soll ich Trumpf spielen etc.? Sie ergibt sich aus dem, beiden Spielern bekannten, Informationsstand. Der Partner hat gemäß den oben beschriebenen Grundprinzipien zu antworten. Die positive Antwort erfolgt durch eine Ansage. Die Anwendung dieses Hilfsmittels setzt keine eindeutig geklärte Parteizugehörigkeit des Fragenden (im Sinne einer eigenen Ansage) voraus.
Es genügt vollkommen, wenn die Parteizugehörigkeit des Fragenden aufgrund des bisherigen Spielverlaufes oder durch den Zeitpunkt des Wartens wahrscheinlich ist! Dies betrifft besonders Gegenansagen. Die Anwendung dieses Hilfsmittels erfordert eine große Portion Selbstdisziplin, da man sich im Anfangsstadium jedes Spieles, bei dem mindestens die Parteizugehörigkeit eines Spielers (Ansage, Hochzeit, Konvention) bekannt ist, nur noch in wenigen Situationen ein längeres Nachdenken erlauben darf. Einen vorläufigen Spielplan entwickelt man sich daher am besten schon bevor man sich bei der Vorbehaltsabfrage gesund meldet!
(Anspiel-)Konventionen
Hiermit sind Anspiele (bis zum letztmöglichen Ansagezeitpunkt) gemeint, die, je nach Verknüpfung mit den Hilfsmitteln 1-3, jeweils immer denselben Informationsgehalt (inkl. Parteizugehörigkeit) besitzen. Sie erfordern häufig eine spezifische Reaktion des Partners. Eine sinnvolle Konvention muß folgende Anforderungen erfüllen:
- Die mit ihr verbundene Information muß auf Dauer für die eigene Partei mehr Vorteile bringen (Steigerung des Erwartungswertes) als eine, durch das Anspiel verursachte, eventuelle Schwächung des eigenen Blattes.
- Sie muß logisch aufgebaut sein, damit es bei den Folgereaktionen nicht zu Mißverständnissen kommt und damit auch unkundige Spieler sie nachvollziehen können.
- Die Wahrscheinlichkeit der Anwendung muß genügend groß sein.
- Die Anfälligkeit gegen Störmanöver der Gegenpartei muß gering sein.
Die folgenden Kapitel zeigen nun, geordnet nach Spieltypen (Normalspiel; Hochzeit; Solo), welche zusätzlichen Möglichkeiten das Doppelkopfspiel durch Verwendung dieser Hilfsmittel erhält. Dabei werden wir immer versuchen anhand von praktischen Beispielen die Ideen dieses Systems und seine Logik anschaulich darzulegen. Selbstverständlich werden wir hinsichtlich der exakten Bedeutung der Hilfsmittel (beispielsweise: Konventionen und Ansagen zum Abbringen vom Normalanspiel) in Abhängigkeit von der genauen Situation unsere eigenen Vorlieben vorstellen. Seid uns also nicht böse, wenn andere Interpretationen nicht zu Wort kommen werden.
Normalspiel
Ein Normalspiel ist durch die folgenden Eigenschaften definiert:
- Eine eindeutige Klärung der Partnerschaften erfolgt durch Ansagen oder Legen der
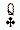 , d. h. der Zeitpunkt der Klärung ist nicht festgelegt.
, d. h. der Zeitpunkt der Klärung ist nicht festgelegt. - Die letztmöglichen Ansagezeitpunkte sind unabhängig vom Spielverlauf.
Andere Spieltypen sind Hochzeiten (Kap. 3) und Soli (Kap. 4). Eine Unterscheidung dieser Typen erscheint sinnvoll, da die vorzeitige Information wer zusammenspielt (vor dem letztmöglichen Ansagezeitpunkt) einen großen Einfluß auf z. B. das Ansageverhalten haben kann.
Erstansage
Eine Erstansage führt (nach TSR) zu einer Erhöhung des Spielwertes um zwei Punkte. Hieraus folgt, daß das Treffen einer Erstansage nur sinnvoll erscheint, wenn das Spiel mit der Ansage in mindestens 50% aller möglichen Kartenverteilungen gewonnen wird. Zur Abschätzung der Gewinnwahrscheinlichkeit stehen das eigene Blatt und die bis zum Ansagezeitpunkt erhaltenen Informationen über die Gesamtkartenverteilung (aus: Spielverlauf und/oder Anspielkonventionen) zur Verfügung. Die folgenden Abschnitte zeigen nun:
- welche Mindestvoraussetzungen für eine Erstansage erfüllt sein sollten und
- welche Möglichkeiten das Essener System zur Beschreibung von besonders starken oder
strukturierten Blättern vorsieht.
Die korrekte Behandlung der Erstansage (inkl. Konventionen) ist für die optimale Ausreizung des Spiels (siehe Kap. 2.2) eminent wichtig, da hier der Partner die entscheidenden Informationen bezüglich Blattstärke und Blattstruktur erhält. Beachte: Das Nichtspielen von bestimmten Varianten verneint automatisch die zugehörige Blattstruktur oder/und Blattstärke!
Stärke der Erstansage
Bei der Entwicklung der Mindestvoraussetzungen sei zunächst von dem Fall ausgegangen, daß zum Zeitpunkt der Erstansage keine außergewöhnlichen Informationen bezüglich der Gesamtkartenverteilung vorliegt. Die Grundlage für die Entscheidung Ansage ja oder nein ist dann lediglich das eigene Blatt. Die Stärke des Blattes wird am besten ausgedrückt durch eine durchschnittlich erreichbare Augenzahl. Die Berechnung dieser Augenzahl erfolgt über die Abschätzung von Erwartungswerten für potentielle Stiche. Der Erwartungswert ist das Produkt aus dem Wert eines Stiches und der Wahrscheinlichkeit diesen Stich tatsächlich zu erhalten. Die folgende Tabelle zeigt ein einfaches Schema zur Abschätzung dieser Werte. Die Angaben beruhen dabei zum einen auf unserer Erfahrung und zum anderen auf den Gesetzen der Stochastik.
Tab. 2: Erwartungswerte für potentielle Stiche
| Potentieller Stich | Wert des Stiches | Wahrscheinlichkeit des
Stiches |
|---|---|---|
| Stechen von ersten Lauf (Chicane) |
= eigene Stechkarte + 20
(genauer: angespieltes As + 2/7 der restlichen Augenzahl der Farbe) |
9/10 (Anmerkung: vgl. Lauf von Fehlkarten) |
| Stechen von zweiten Lauf (Singleton) |
= eigene Stechkarte + 10 bis 25
Beachte: Der Wert hängt stark vom ersten Lauf ab |
1/2 (bei Chicane = 2/3)
Beachte: Die Wahrscheinlichkeit wird durch den ersten Lauf beinflußt. |
| Stechen von Lauf (Chicane) |
= eigene Stechkarte + 15
(genauer: angespieltes As + 2/5 der restlichen Augenzahl der Farbe) |
3/4 |
| Besitz von |
~20 - 30 (hängt von der
Möglichkeit des Einsatzes der Karte ab) |
1 |
| Besitz von |
~ 15 - 20 (in Kombination mit |
3/4 (Schätzung) |
| Besitz von |
~ » 20 - 25 (in Kombination mit Weitere Damen erhöhen diesen
Wert nur noch geringfügig.
Genauso sind einzelne |
3/4 (Schätzung) |
| Anspielasse:
Anmerkung: + bezieht sich auf die sonstigen Handkarten in dieser Farbe
also: z.B: |
für = 11 + 3/Anzahl der fehlenden
Karten der Farbe x (50 - eigene
Augenzahl der Farbe)
für |
Die Angaben gelten nur für ein As. Das nächste As läuft mit dem Produkt der Werte der Einzelwahrscheinlichkeiten. |
Die Angaben für die Wahrscheinlichkeiten des Stiches sind im Sinne einer einfachen Berechnung auf einfache Werte (1, 9/10, 3/4, 2/3, 1/2, 1/4) gerundet. Aus dem gleichen Grund wird auch bei der Angabe der Stichwerte häufig mit einfachen Werten (10, 15, 20, 25, 30) operiert. Genauere Werte können aus den Tabellen in Kap 5 berechnet werden. Die Gesamtstärke eines Blattes ergibt sich aus der Summe aller Einzelerwartungswerte. Statistische Auswertungen verschiedener Einladungsturniere (Deutschlandpokal Braunschweig 1991, Dodge-Mannschaftsturnier München 1992 und 1. Dullenknicken Essen 1993) haben gezeigt, daß ein Re-Spieler durchschnittlich eine Augenzahl von etwa 68 und ein Kontra-Spieler durchschnittlich eine Augenzahl von etwa 52 pro Spiel erzielt. Für eine Erstansage sollte der Gesamterwartungswert des eigenen Blattes zum einen so groß sein, daß mit einem knapp unter Durchschnitt liegenden Blatt des Partners die Gewinnwahrscheinlichkeit etwas mehr als 50% beträgt, und zum anderen sollte er im Hinblick auf weitere Ansagen größer als der durchschnittliche Erwartungswert eines Spielers der jeweiligen Partei sein. Hieraus folgt für die Mindestblattstärke für eine Erstansage:
* RE: >= 75 Augen und * KONTRA: >= 85 Augen.
Für die Entscheidung Ansage ja oder nein zählt die bis zur Ansage erzielte Augenzahl plus Summe der Einzelerwartungswerte (siehe Tab. 2). Hierdurch wird klar, daß es i.d.R. besser ist bis zum letztmöglichen Zeitpunkt mit der Ansage zu warten, da ansonsten Informationen, die eine Neuberechnung der Erwartungswerte bedingen, unnötigerweise verlorengehen. Es gibt nur zwei Ausnahmen:
- Es wird Trumpf angespielt und der Ansagende legt
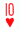 (Die Ansage erfolgt sofort, da keine Neubewertung möglich ist und der Partner die Gelegenheit zum Unterbringen von
(Die Ansage erfolgt sofort, da keine Neubewertung möglich ist und der Partner die Gelegenheit zum Unterbringen von 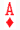 oder
oder 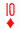 hat).
hat).
- Es liegen 2 Volle und die Stechkarte ist ebenfalls ein Voller (Hier erfolgt ebenfalls sofort eine Ansage wegen der Chance auf einen Doko und der geringen Gefahr des Verlustes des
Stiches [< 5%] ).
Nun aber zu einigen Blattbeispielen, die das Bewertungsschema etwas verdeutlichen sollen: (...)
Die Orginal Beispiele sind in einer "auhfgehübscht Form" zu finden unter:Erwartungswerte
Die Beispiele sollten zeigen, wie mit Hilfe des obigen Schemas die Blattstärke abgeschätzt wird. Gleichzeitig ist dabei auf einige Schwächen aufmerksam gemacht worden. Eine Einschätzung eines Wertes für Trumpflänge bzw. -kürze fehlt. Auch sind die Angaben für das Stechen von Farben relativ ungenau, da die Wahrscheinlichkeiten zum einen davon abhängen, was im ersten Stich in der Farbe gefallen ist und zum anderen davon abhängen, ob der betreffende Spieler eine Ansage getätigt hat (mit Ansage erhöhen sich die Wahrscheinlichkeiten etwas). Bei allen Bättern sollte die Erstansage zum letztmöglichen Zeitpunkt getroffen werden, da die volle Information des Spielverlaufes für die Entscheidung, ob überhaupt eine Erstansage getroffen werden kann, benötigt wird. Folgende Spielverläufe führen zu einer Abwertung der Blattstärke und können zum Verzicht einer Erstansage führen:
- Das selbst angespielte As wird gestochen oder man wird überstochen.
- Der erste Lauf einer Farbe, die man im zweiten Lauf stechen will wird hinter dem Spieler beim ersten Lauf gestochen oder es fällt direkt hinter dem Spieler das As (Verringerung der Wahrscheinlichkeit) oder der Stich wird extrem fett (Wert des zweiten Stiches sinkt).
- Ein anderer Spieler macht die ersten beiden Stiche: Hierdurch sinkt der durchschnittliche Wert des Partnerblattes, da der Spieler mit höherer Wahrscheinlichkeit Gegner ist (besonders wenn der Spieler RE ansagen wollte). Daraus folgt: Für eine Erstansage ist ein stärkeres Blatt erforderlich.
- Es erfolgt eine Ansage der Gegenpartei vor der eigenen Ansage (siehe Kap. 2.3).
In besondern Situationen kann eine Erstansage auch mit Blättern erfolgen, die knapp unter den Erfordernissen für eine Erstansage liegen. Hierzu ist allerdings notwendig, daß der Spieler zu diesem sehr frühen Zeitpunkt abschätzen kann, daß alle anderen Spieler ein ungefähr gleich starkes Blatt halten und somit sein eigenes Blatt, welches nur noch knapp über dem Durchschnitt liegt zum Gewinn ausreichen sollte. Die Gefahr bei einer solchen Ansage ist allerdings, daß der Partner mit einem wesentlichen stärkeren Blatt rechnet und somit eine weitere Ansage trifft.
Daher sollte von diesem Typ der Ansage nur sehr spärlich an Position 3 oder 4 (verringert das Risiko einer weiteren Ansage des Partners) Gebrauch gemacht werden. Ein Beispiel:
Blatt 1: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Position 2)
1.Stich:
(Position 2)
1.Stich: ![]()
![]()
![]()
![]() 2.Stich:
2.Stich: ![]()
![]() +RE <
+RE <![]() >
>![]()
Anmerkung: "<>" = Aufspiel --Solmyr 15:22, 24. Apr. 2009 (CEST)
Nach der bisherigen Blattbewertung besitzt Spieler 2 kein Blatt für eine Erstansage
(Erwartungswert > 68). In dieser besonderen Situation sollte Spieler 2 allerdings aus
folgender Überlegungen trotzdem RE ansagen: Mit Spieler 1 oder 3 als Partner hat die
eigene Partei schon einen Stich, wobei Spieler 1 zusätzlich noch in ![]() anschieben kann. Außerdem scheint keiner der Spieler ein über ein starkes Blatt zu verfügen (keine Ansage).
anschieben kann. Außerdem scheint keiner der Spieler ein über ein starkes Blatt zu verfügen (keine Ansage).
Bei stärkeren als den bisher beschriebenen Blättern sieht die Situation anders aus: Stärkere
Blätter sind immer gekennzeichnet durch Trumpflänge (>= 8 = wenige Fehlverlierer) und Trumpfstärke (Minimum: ~ ![]()
![]()
![]()
![]() oder
oder ![]()
![]()
![]() oder bei Kontra-Partei
oder bei Kontra-Partei ![]()
![]()
![]()
![]() ).
).
Die Zahl 8 als Definition für Trumpflänge kommt dadurch zustande, daß die Wahrscheinlichkeit, daß kein anderer Spieler eine gleiche oder höhere Trumpfanzahl als dieser Spieler besitzt gerade bei 8 Trumpf über 50% liegt. Eine Abschätzung nach dem bekannten Schema ist nur bedingt möglich, da die Trumpfstärke nur ungenau in eine durchschnittliche Augenzahl umgerechnet werden kann. Sie sollte aber für einen Re-Spieler bei > 100 und bei einem KONTRA-Spieler > 110 liegen. Besser erscheint in diesem Zusammenhang eine Verliererrechnung].
Ein starkes Blatt sollte maximal 4 Verlierer besitzen. Wir unterscheiden zwischen ganzen und halben Verlierern:
* Ganze Verlierer:
Jede fehlende ![]() und die erste Karte von
und die erste Karte von ![]() /
/![]() (außer angespieltes As bzw. Doppelasse).
(außer angespieltes As bzw. Doppelasse).
* Halbe Verlierer:
Jede fehlende ![]() (
(![]() bei KONTRA-Ansagen bzw. 2
bei KONTRA-Ansagen bzw. 2 ![]() bei RE-Ansagen),
die zweite Karte von
bei RE-Ansagen),
die zweite Karte von ![]() /
/![]() , die erste Karte von
, die erste Karte von ![]() , Doppelasse und angespieltes As.
, Doppelasse und angespieltes As.
Hier erfolgt die Ansage bei Legen der ersten eigenen Karte (Ausnahme Anfragen).
Der Nachteil durch den mit der vorzeitigen Ansage verbundenen Informationsverzicht wird überkompensiert durch die Tatsache, daß der Partner nunmehr auch mit schwächeren Blättern eine
weiterführende Ansage treffen kann. Vor allen Dingen kann der Partner bisher unbedeutende
Trumpfkarten wie rote Damen oder eine ![]() aufwerten. Auf eine KONTRA-Ansage bei Legen der ersten Karte wird häufig verzichtet.
aufwerten. Auf eine KONTRA-Ansage bei Legen der ersten Karte wird häufig verzichtet.
Dies geschieht aus zwei Gründen:
- Die Wahrscheinlichkeit, daß der Partner ein Blatt hält welches die keine 90-Ansage ermöglicht,
ist geringer als bei dem RE-Partner.
- Die Wahrscheinlichkeit, daß ein Spieler der Gegenpartei eine knappe Ansage auf der Hand
hält, ist höher als bei einem starken RE-Spieler. In einigen Fällen wird nachträglich ein starkes
KONTRA-Blatt deklariert. So kann z.B. bei eigenem Anspiel von klein Trumpf (Blatt: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ), wobei an beliebiger Position eine
), wobei an beliebiger Position eine ![]() ohne
Ansage fällt, nun als Kommentar zur
ohne
Ansage fällt, nun als Kommentar zur ![]() KONTRA angesagt werden, da nun eine Ansage
eines anderen Spielers sehr unwahrscheinlich ist.
KONTRA angesagt werden, da nun eine Ansage
eines anderen Spielers sehr unwahrscheinlich ist.
(...) Beispiele fehlen
Neben den bisher beschriebenen Ansagezeitpunkten sieht das Essener System noch eine RE-Ansage vor Anspiel der ersten Karte vor. Der Spieler zeigt damit, daß er definitiv angespielt werden kann. Hierzu muß er ![]()
![]() (an Position 2 auch eine
(an Position 2 auch eine ![]() ) besitzen. Die Ansage charakterisiert ein starkes RE-Blatt. Es muß nicht unbedingt Asse enthalten. Der anspielende Partner ist nicht verpflichtet Trumpf anzuspielen. Spielt er ein As an, so zeigt er seine eigene Stärke analog dem vorherigen Beispiel durch die Wahl des Ansagezeitpunktes (mit Anspiel= sehr stark; vor Legen der Karte des starken Spielers = Blatt mit Zusatzwerten; keine Ansage = schwach). Das angespielte As sollte allerdings eine Laufwahrscheinlichkeit von mindestens 66% (siehe Anhang Tab. A3) besitzen.
) besitzen. Die Ansage charakterisiert ein starkes RE-Blatt. Es muß nicht unbedingt Asse enthalten. Der anspielende Partner ist nicht verpflichtet Trumpf anzuspielen. Spielt er ein As an, so zeigt er seine eigene Stärke analog dem vorherigen Beispiel durch die Wahl des Ansagezeitpunktes (mit Anspiel= sehr stark; vor Legen der Karte des starken Spielers = Blatt mit Zusatzwerten; keine Ansage = schwach). Das angespielte As sollte allerdings eine Laufwahrscheinlichkeit von mindestens 66% (siehe Anhang Tab. A3) besitzen.
Die gleiche Ansage wird als KONTRA-Spieler nicht angewandt,da das Signalisieren der ![]()
![]() eher für die RE-Partei nützlich ist. Sie wissen, daß der Partner des starken KONTRA-Spielers keine Kontrolle in Trumpf besitzt, was bei dem Partner eines starken RE-Spieler nicht der Fall wäre.
eher für die RE-Partei nützlich ist. Sie wissen, daß der Partner des starken KONTRA-Spielers keine Kontrolle in Trumpf besitzt, was bei dem Partner eines starken RE-Spieler nicht der Fall wäre.
90-Anfragen
Eine Anfragesituation liegt immer dann vor, wenn ein Spieler, der eine Erstansage getroffen hat, vor Legen der eigenen Karte zu einem Stich einige Sekunden wartet. Er tut dies, um seinem Partner die Möglichkeit einer weiteren Ansage zu geben, wenn er diesen Stich wahrscheinlich macht oder wenn er angespielt werden kann (links vom Anfragenden aus gesehen sitzend). Voraussetzung für eine Anfrage sind ein starkes Blatt (Minimum: Stärke für eine RE/KONTRAAnsage bei Legen der ersten Karte) und ein echter Vorteil für die eigene Partei durch die Antwort, welche durch das Treffen der nächsten Ansage erfolgt.
Echte Vorteile sind zum Beispiel:
- Abwurf eines Fehlverlierers in einer anderen als der angespielten Farbe (Abwurf sollte Singleton sein).
- Schmieren eines Fehlvollen in der angespielten Farbe (z. B. bei 10, 9).
- Bedienen mit erkennbaren Singleton (K oder 9, meist an Position 4, fordert das Nachspiel der Farbe).
- Verhindern der Verschwendung eines hohen Trumpfes (an Position 3, wenn zwei kleine Trumpf liegen).
- Abwurf einer Stehkarte (zeigt Partner ein 0-Fehlverliererblatt = wichtige Information).
Wir unterscheiden zwischen forcierenden und einladenden Anfragen.
Eine forcierende Anfrage darf nur mit Blättern gestellt werden, die neben dem echten Vorteil so stark sind, daß auch mit
einem sehr schwachen Blatt (z.B.: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , Anfrage auf
, Anfrage auf
![]() ) des Antwortenden eine reelle Chance besteht die Ansagen zu erfüllen. Hierbei muß der
Anfragende auch mit einer nicht ganz normalen Fehlverteilung rechnen. Der gefragte Partner ist
zur Antwort verpflichtet (keine Antwort = kein Partner). Eine Einschätzung hinsichtlich der
Punktstärke ist kaum möglich. Der anfragende Spieler sollte allerdings nach der Antwort max. 2-
2,5 Verlierer (bei guten Trumpfmittelkarten = rote Damen und schwarze Buben) besitzen. Die
Trumpfstärke sollte oberhalb des für die Erstansage mit Legen der ersten eigenen Karte notwendigen
Minimums liegen (z.B.:
) des Antwortenden eine reelle Chance besteht die Ansagen zu erfüllen. Hierbei muß der
Anfragende auch mit einer nicht ganz normalen Fehlverteilung rechnen. Der gefragte Partner ist
zur Antwort verpflichtet (keine Antwort = kein Partner). Eine Einschätzung hinsichtlich der
Punktstärke ist kaum möglich. Der anfragende Spieler sollte allerdings nach der Antwort max. 2-
2,5 Verlierer (bei guten Trumpfmittelkarten = rote Damen und schwarze Buben) besitzen. Die
Trumpfstärke sollte oberhalb des für die Erstansage mit Legen der ersten eigenen Karte notwendigen
Minimums liegen (z.B.: ![]()
![]()
![]() + eine rote Dame oder
+ eine rote Dame oder ![]()
![]() + mind. 2 rote Damen + 2 schwarze Buben etc.). Bei einer einladenen Anfrage (» 2,5-3 Verlierer bei etwas
niedrigerer Trumpfstärke bzw. schlechteren Trumpfmittelkarten) darf der Partner mit einem Nullblatt hingegen die Antwort verweigern. In beiden Fällen hat der Anfragende die Verantwortung für die Ansage des Partners übernommen. Der gefragte Spieler sollte auf das Urteilsvermögen des fragenden Spielers vertrauen. Der anfragende Spieler sollte eventuelle Nachspielprobleme des Partners berücksichtigen.
+ mind. 2 rote Damen + 2 schwarze Buben etc.). Bei einer einladenen Anfrage (» 2,5-3 Verlierer bei etwas
niedrigerer Trumpfstärke bzw. schlechteren Trumpfmittelkarten) darf der Partner mit einem Nullblatt hingegen die Antwort verweigern. In beiden Fällen hat der Anfragende die Verantwortung für die Ansage des Partners übernommen. Der gefragte Spieler sollte auf das Urteilsvermögen des fragenden Spielers vertrauen. Der anfragende Spieler sollte eventuelle Nachspielprobleme des Partners berücksichtigen.
Bei Anfragen werden nun die folgenden Situationen unterschieden:
1.) Erstansage im ersten Stich direkt vor Legen der eigenen Karte und Warten.
Die Anfrage ist forcierend, d.h. erhält der Partner wahrscheinlich diesen Stich (angespieltes As
oder er kann stechen), so hat er dies durch die keine 90-Ansage zu erkennen zu geben.
Folgendes sind Blätter für eine forcierende Anfrage: (...)
2.) Erstansage bei Anspiel der ersten Karte (nur bei Fehlkarte) und Warten vor Legen der ersten eigenen Karte.
Die Anfrage ist lediglich einladend, d.h. der Partner, der diesen Stich wahrscheinlich macht, darf mit einem sehr schwachen Blatt die Antwort verweigern. Für eine Antwort sollte er 1-2 zusätzliche Stiche mitbringen oder Trumpflänge (³ 7). Die Anfrage darf nur gestellt werden, wenn der anfragende Spieler die angespielte Farbe stechen kann. Ein Partner, der den Stich nicht macht, soll die Möglichkeit erhalten sich durch Schmieren eines Vollen (i.d.R. eine 10) zu zeigen. (...)
3.) Erstansage mit Legen der ersten eigenen Karte und Warten vor Legen der zweiten eigenen Karte.
Die Anfrage hat zweifachen Charakter: Für den Spieler, der wahrscheinlich die beiden Stiche
erhält, ist sie forcierend. Für den Spieler, der lediglich den zweiten Stich wahrscheinlich erhält ist
sie nur einladend. Der anfragende Spieler zeigt zunächst eine starke Erstansage. Er besitzt jedoch
erst beim zweiten Anspiel einen echten Vorteil durch die Anfrage. Er könnte beispielsweise
ein Blatt mit 9 Trumpf (![]()
![]()
![]()
![]() an der Spitze) und
an der Spitze) und ![]()
![]()
![]() als Fehlkarten besitzen.
Auf ein angespieltes
als Fehlkarten besitzen.
Auf ein angespieltes ![]() kann er keine Anfrage stellen, da das Blatt für eine forcierende Anfrage zu schwach ist. Wird
kann er keine Anfrage stellen, da das Blatt für eine forcierende Anfrage zu schwach ist. Wird ![]() nachgespielt oder in
nachgespielt oder in ![]() angeschoben, so besitzt er nun einen echten
Vorteil. Bei
angeschoben, so besitzt er nun einen echten
Vorteil. Bei ![]() ist die Anfrage forcierend für den anspielenden Spieler, andernfalls lediglich
einladend.
ist die Anfrage forcierend für den anspielenden Spieler, andernfalls lediglich
einladend.
4.) Erstansage direkt vor Legen der zweiten eigenen Karte und Warten. Dies ist eine aus der Spielsituation geborene spezielle Anfrage, zumeist an den Spieler der eine für den fragenden Spieler besonderes nützliche Stärke in seinem Blatt zeigt. Sie ist, da der anfragende Spieler bereits ein besonders starkes Blatt verneint hat (keine Ansage bei Legen der ersten eigenen Karte), nur einladend. Ein klassisches Beispiel: (...)
(Anspiel-)Konventionen
Unter Konventionen verstehen wir Anspiele, die in Verbindung mit den anderen Hilfsmitteln des Essener Systems (meist Ansagezeitpunkt) jeweils immer den gleichen Informationsgehalt besitzen. Die mit diesen Konventionen verbundene Idee ist dem Partner schnell ein Maximum an wichtigen Informationen über das eigene Blatt zur Verfügung zu stellen, damit dieser dann in Verbindung mit seinem eigenen Blatt das Spielziel festlegen kann. Bei der Anwendung von (Anspiel-)Konventionen ist gegenseitiges Vertrauen in die Glaubwürdigkeit und das Urteilungsvermögen des Partners gefragt. Das Essener System kennt im wesentlichen zwei konventionelle Anspiele, die natürlich den Anforderungen einer guten Konvention (hoher Informationsgehalt, Logik, hohe Anwendungswahrscheinlichkeit, geringe Störanfälligkeit) genügen. Dies haben zumindest unsere praktischen Erfahrungen, unabhängig von der Art der Turniere (Vereins-, offene und Einladungsturniere), gezeigt.
Herz 10 Anspiel-Konvention
1. Herz 10 Anspiel-Konvention:
Das Anspiel einer ![]() (bis zum letztmöglichen Ansagezeitpunkt) zeigt den Besitz einer
(bis zum letztmöglichen Ansagezeitpunkt) zeigt den Besitz einer ![]() und
einer
und
einer ![]() (in seltenen Fällen auch
(in seltenen Fällen auch ![]() und Doppel-
und Doppel-![]() ). Je nachdem ob bzw. wann eine Ansage
erfolgt liegt eine unterschiedliche Stärke des Blattes vor. Die Idee dieser, sowie auch anderer
Anspielkonventionen (
). Je nachdem ob bzw. wann eine Ansage
erfolgt liegt eine unterschiedliche Stärke des Blattes vor. Die Idee dieser, sowie auch anderer
Anspielkonventionen (![]() ,
, ![]() ) ist es dem Partner, anstelle von knappen eigenen Ansagen (i.d.R.
RE oder 90) durch Übermittlung von Struktur und Stärke des eigenen Blattes die Entscheidung
einer Erstansage zu überlassen oder eine weitergehende Ansage (90, 60 etc.) mit höherer
Sicherheit zu ermöglichen (für eine 90-Ansage benötigt man eine Sicherheit von 90%!). Der
Anspieler erhält hier durch Ansage oder auch durch Schmieren eines Karo-Vollen die Information,
wo sein Partner sitzt bzw. ob er die andere
) ist es dem Partner, anstelle von knappen eigenen Ansagen (i.d.R.
RE oder 90) durch Übermittlung von Struktur und Stärke des eigenen Blattes die Entscheidung
einer Erstansage zu überlassen oder eine weitergehende Ansage (90, 60 etc.) mit höherer
Sicherheit zu ermöglichen (für eine 90-Ansage benötigt man eine Sicherheit von 90%!). Der
Anspieler erhält hier durch Ansage oder auch durch Schmieren eines Karo-Vollen die Information,
wo sein Partner sitzt bzw. ob er die andere ![]() besitzt. Es werden 3 Situationen unterschieden:
1. Ansage mit Legen der ersten eigenen Karte und Anspielen von
besitzt. Es werden 3 Situationen unterschieden:
1. Ansage mit Legen der ersten eigenen Karte und Anspielen von ![]() spätestens zum dritten
Stich.
Bedeutung: Mein Blatt ist so stark, daß mir eine
spätestens zum dritten
Stich.
Bedeutung: Mein Blatt ist so stark, daß mir eine ![]() beim Partner ausreicht die Gegenpartei
unter 90 zu spielen. Der Partner sollte sofort beim Anspiel der
beim Partner ausreicht die Gegenpartei
unter 90 zu spielen. Der Partner sollte sofort beim Anspiel der ![]() keine 90 ansagen, wenn er
die andere
keine 90 ansagen, wenn er
die andere ![]() besitzt unabhängig von der Stärke seines eigenen Blattes (einzige Ausnahmen
sind
besitzt unabhängig von der Stärke seines eigenen Blattes (einzige Ausnahmen
sind ![]()
![]() bzw.
bzw. ![]()
![]() x als Trumpf; hier sollte der Spieler jeweils
x als Trumpf; hier sollte der Spieler jeweils![]() legen!). Der Erstansager
könnte eines der folgenden Blätter auf der Hand halten:
legen!). Der Erstansager
könnte eines der folgenden Blätter auf der Hand halten:
(...) Vergleiche auch: Herz 10 Anspiel-Konvention
2. Anspiel der ![]() zum ersten oder zweiten Stich ohne Ansage.
zum ersten oder zweiten Stich ohne Ansage.
Bedeutung: Mein Blatt ist leidlich trumpfstark (6-8 [meist 7] Trumpf mit ![]()
![]()
![]() an der
Spitze), besitze allerdings nur Zusatzwerte, die ich dem Partner vor Legen seiner elften Karte
zeigen kann. Beispielblätter: (...)
an der
Spitze), besitze allerdings nur Zusatzwerte, die ich dem Partner vor Legen seiner elften Karte
zeigen kann. Beispielblätter: (...)
3. Anspiel der ![]() zum ersten oder zweiten Stich mit Ansage (RE) zum letzten Zeitpunkt.
zum ersten oder zweiten Stich mit Ansage (RE) zum letzten Zeitpunkt.
Bedeutung: Ich besitze ein Blatt, daß die schon beschriebene Trumpfstruktur besitzt, welches aber in der Stärke zwischen den schon beschriebenen Blättern liegt. Man besitzt noch Zusatzwerte, die der Partner bis zum Legen seiner elften Karte nicht kennt. Diese könnten sein: Stechen einer Farbe, weitere Anspielasse, ein Doppelas, 9 Trumpf oder 8 gute Trumpf etc.. Beispiele:
(...)
Kreuz Dame/Pik Dame - Anspiel-Konvention:
Das Anspiel von ![]() /
/![]() deklariert einen RE-Spieler mit Doppel-
deklariert einen RE-Spieler mit Doppel-![]() . Analog der
. Analog der ![]() -Anspiel-
Konvention zeigt der Ansagezeitpunkt wiederum die Stärke des Blattes. Diese Konvention erfordert
keine spezifische Reaktion des Partners.
1) Ansage mit Legen der ersten Karte und Anspiel von
-Anspiel-
Konvention zeigt der Ansagezeitpunkt wiederum die Stärke des Blattes. Diese Konvention erfordert
keine spezifische Reaktion des Partners.
1) Ansage mit Legen der ersten Karte und Anspiel von ![]() /
/![]() bis spätestens zum dritten Stich.
bis spätestens zum dritten Stich.
Bedeutung: Der Spieler besitzt ein starkes RE-Blatt (siehe auch Erstansage Kap. 2.1.1) und mit
minimalen Zusatzwerten des Partners (z.B. ![]() , zwei Anspielasse) ist die keine 90-Ansage möglich.
Die Entscheidung trifft der Partner, sofern er bei dem Stich für die keine 90-Ansage nicht vor
dem starken RE-Spieler sitzt und keine Zusatzwerte mehr auf der Hand hält. Beispiele:
(...)
, zwei Anspielasse) ist die keine 90-Ansage möglich.
Die Entscheidung trifft der Partner, sofern er bei dem Stich für die keine 90-Ansage nicht vor
dem starken RE-Spieler sitzt und keine Zusatzwerte mehr auf der Hand hält. Beispiele:
(...)
2) Anspiel von ![]() /
/![]() zum ersten oder zweiten Stich ohne Ansage.
zum ersten oder zweiten Stich ohne Ansage.
Bedeutung: Der Spieler besitzt ein trumpfkurzes Blatt (5-6, selten schwache 7) ohne Zusatzwerte, die der Partner vor Legen seiner elften Karte nicht erkennen kann. Beispiele: (...)
3) Anspiel von ![]() /
/![]() zum ersten oder zweiten Stich mit Ansage zum letzten Zeitpunkt.
zum ersten oder zweiten Stich mit Ansage zum letzten Zeitpunkt.
Bedeutung: Der Spieler besitzt ein Blatt mit Doppel-![]() und im Gegensatz zu 2) noch Zusatzwerte,
die der Partner vor Legen seiner elften Karte nicht erkennen kann. Zusatzwerte sind die
gleichen wie bei der
und im Gegensatz zu 2) noch Zusatzwerte,
die der Partner vor Legen seiner elften Karte nicht erkennen kann. Zusatzwerte sind die
gleichen wie bei der ![]() -Anspiel-Konvention, wobei hier allerdings schon 7 gute Trumpf mit
Singleton in einer schwarzen Farbe oder 8 schlechte Trumpf für die Ansage ausreichen.
Beispiele: (...)
-Anspiel-Konvention, wobei hier allerdings schon 7 gute Trumpf mit
Singleton in einer schwarzen Farbe oder 8 schlechte Trumpf für die Ansage ausreichen.
Beispiele: (...)
Optimierung (Ausreizen) des Spieles
Problematik der Optimierung
Das Ziel der Optimierung ist es herauszufinden, welche Ansage im Spiel gerade noch mit der notwendigen Sicherheit (keine 90 ³ 88,89%; keine 60 ³ 91,67%; keine 30 ³ 93,33%; Schwarz ³ 94,74% vergleiche Tab. 1 Seite 5) erfüllt werden kann. Der erste und wichtigste Schritt ist die systemgerechte Behandlung der Erstansage (Ansagezeitpunkte, Anfragen, [Anspiel- ]Konventionen). Auf dieser Basis erfolgt dann der weitere Informationsaustausch. Für das Treffen von weiteren Ansagen (insbesondere keine 60, keine 30, schwarz) muß möglichst rasch herausgefunden werden, wieviele Verlierer das gemeinsame Blatt besitzt. Wir unterscheiden zwischen Trumpf- und Fehlverlierer: (...)
Hilfsmittel
Folgeansagen und Ansagezeitpunkte
1) Beantwortung von 90-Anfragen: (...) 2) Warnung des Partners (...) 3) Informationsübermittlung (...)
Anfragen
1) Anfragen bei ungeklärter Partnerschaft (siehe Kap. 2.1.2 und 2.2.2.1).
2) Anfragen bei (wahrscheinlich) geklärter Partnerschaft.
Die Idee einer solchen Anfrage ist es eine spezielle Information vom Partner zu bekommen. Dies können sein:
- Besitzt du eine bestimmte Karte (i.d.R. höchster Trumpf oder gleicher wie angespielter)?
- Stichst du diese Fehlkarte?
- Soll ich Trumpf oder Fehl spielen?
Der fragende Spieler garantiert bei positiver Antwort (= weitere Ansage) für die notwendige Sicherheit für diese Ansage. Die Anfragen werden gestellt, indem vor dem eigenen Anspiel oder Legen der eigenen Karte (häufig bei Fehlanspielen der Gegner, wo der eigene Partner im Stich hinter einem selbst sitzt) gewartet wird. Das Warten simuliert ein Nachdenken, ob eine weitere Ansage möglich ist. Hieraus folgt, daß der Partner, wenn er offensichtlich den Knackpunkt der Überlegungen seines Partners abdeckt, logischerweise eine weitere Ansage treffen kann. Die Art der Frage wird dann aus der zuvor gelegten Karte (häufig bei hohem Trumpf und Warten vor dem Anspiel) oder durch die dann gelegte Karte, immer im Gesamtzusammenhang mit dem Spiel gesehen, deutlich. Hieraus folgt, daß der Partner nicht unbedingt sofort auf das Warten hin antworten kann. Viele Beispiele an dieser Stelle erscheinen nicht sinnvoll, da häufig einige Stiche (also ein hoher Informationsgehalt) zur Interpretation einer solchen Anfrage notwendig sind. Daher an dieser Stelle nur zwei Beispiele (weitere folgen bei der Diskussion der Partiebeispiele (...)
Regeln für den Informationsaustausch
In den bisherigen Kapiteln zur Optimierung (Ausreizen) des Spieles wurden vielfach Beispiele angeführt, in denen die Prinzipien und Regeln für den weiterführenden Informationsausstausch (nach der Erstansage bzw. Anfrage oder Konvention) angeklungen sind. Wir wollen sie an dieser Stelle noch mal zusammenfassen:
Die Initiative liegt beim Ausreizen eines Spieles zunächst immer bei dem Spieler, über dessen Blatt sein Partner weniger Informationen besitzt (zumeist beim schwächeren Spieler). (...)
Beispiele
(...)
Gegenansagen
Grundlagen
Eine Gegenansage erhöht den Spielwert analog einer Erstansage um zwei Punkte. Dies bedeutet allerdings nicht, daß eine Gegenansage nur sinnvoll erscheint, wenn die Gewinnaussichten der eigenen Partei > 50% (vergleiche Tab. 1) liegen. Selbst bei einer Erwiderung auf eine Erstansage ist dies nicht immer der Fall. Bei Gegenansagen auf weitere Ansagen reicht häufig eine Erhöhung der Gewinnwahrscheinlichkeit (siehe Tab. 1) aus. Grundsätzlich sollte der Spieler, der eine Gegenansage plant, bedenken, daß die Gegenansage einen entscheidenden Einfluß auf den weiteren Spielverlauf und somit Spielausgang haben kann. Er muß beurteilen, ob die Information für den eigenen Partner wichtiger als für die Gegenpartei ist. Gegenansagen sollten daher nur bei Besitz der Initiative oder mit stärkeren Blättern gemacht werden. Im ersteren Fall ist die Information für den Partner i.d.R. wichtiger und im zweiten Fall kompensiert die Stärke die Warnung, die die Gegenpartei erhält. Dies zeigt schon, daß das Treffen einer Gegenansage sehr stark situationsabhängig ist. Aus diesem Grund läßt sich auch keine notwendige Punktstärke für eine Gegenansage postulieren. Bei der Überlegung Gegenansage ja oder nein sollte sich der Spieler folgende Fragen beantworten:
* Wie stark sind die Ansagen der Gegenpartei ?
Antworten hierauf gibt das Kapitel Erstansage und Optimierung (Ausreizen) des Spiels. Es dürfte einleuchtend sein, daß gegen ein RE/KONTRA mit Legen der ersten Karte oder einer Anfrage das eigene Blatt für eine Gegenansage nur so vor Kraft strotzen muß. Hingegen darf das eigene Blatt bei normalen Ansagen ruhig etwas schwächer sein.
* Welche Informationen sind mit den Ansagen der Gegenpartei verbunden?
Siehe ebenfalls Anmerkungen Punkt 1. Ein simples Beispiel: Es macht schon etwas aus, ob
der RE-Partner auf eine angespielte ![]() sofort RE ansagt oder erst nachdem ein As nachgespielt
wurde. Für den Fall, daß man selbst keine
sofort RE ansagt oder erst nachdem ein As nachgespielt
wurde. Für den Fall, daß man selbst keine ![]() besitzt, weiß man im zweiten Fall,
daß sie mit hoher Wahrscheinlichkeit beim Partner sitzt.
besitzt, weiß man im zweiten Fall,
daß sie mit hoher Wahrscheinlichkeit beim Partner sitzt.
- Wie ist der bisherige Spielverlauf für die Gegenpartei zu bewerten?
Der Spieler beurteilt hier, ob der Spielverlauf den Erwartungen der erstansagenden Partei jeweils bis zu der jeweiligen Ansage entspricht oder nicht. Die ausreichende Stärke des eigenen Blattes für eine Gegenansage muß natürlich bei einem positiven Spielverlauf der Gegenpartei wesentlich höher sein als bei einem negativen Spielverlauf.
Hier einige Spielverläufe, die dieser Aspekt beleuchten: (...)
Hilfsmittel
Ansagezeitpunkte
Eine vorzeitige Ansage hat im wesentlichen zwei Bedeutungen.
- Sie dient zur Klärung der Partnerschaft oder als Kommentar zur angespielten Farbe oder Trumpf.
- Der Spieler zeigt, daß er angespielt werden kann bzw. daß er den Stich wahrscheinlich machen wird.
Einige Beispiele: (....)
Anfragen
Anfragen bei der Gegenansage werden gestellt mittels Warten vor Legen der eigenen Karte oder vor dem eigenen Anspiel. Das Ziel ist es herauszufinden, ob der Partner (bzw. die eigene Partei siehe Situation 1 etwas weiter oben) den Stich, bei dem gewartet wird, macht bzw. ob er angespielt werden kann. Eine solche Anfrage setzt voraus, daß die eigene Parteizugehörigkeit durch den bisherigen Spielverlauf oder durch die Situation, in der überlegt wird, zumindest wahrscheinlich ist. Gelegentlich wird die Bedeutung und Parteizugehörigkeit der Anfrage erst durch die gelegte Karte klar. Für den gefragten Spieler gelten die schon bekannten Regeln. Die Anfragen sind i.d.R. forcierend. Das Stellen einer solchen Anfrage führt zu einer Erhöhung der Gewinnaussichten für eine Gegenansage, daß heißt der anfragende Spieler besitzt zumeist einen echten Vorteil. Die Stärke hängt von den bekannten Faktoren Informationsstand des Spiels (Fragen 1-4) und der Struktur des eigenen Blattes ab. Diese Art der Anfrage ist vielfach unbekannt.
Daher an dieser Stelle eine etwas größere Zahl von instruktiven Beispielen: (...)
Hochzeit
Bei der Hochzeit besteht zwar die gleiche Kartenhierachie wie bei einem Normalspiel (im Gegensatz zum Solo), trotzdem erscheint uns ein gesondertes Kapitel notwendig. Es bestehen Unterschiede im Zeitpunkt der Partnerschaftsklärung und der Ansagezeitpunkte. Hieraus ergeben sich einige gesonderte Aspekte im Hinblick auf die Anwendung des Essener Systems. Die Hochzeit ist durch folgende Eigenschaften charakterisiert:
- Eine eindeutige Klärung der Partnerschaften erfolgt bis spätestens im dritten Stich, ohne
daß eine Ansage erfolgt bzw. eine ![]() gelegt werden muß.
gelegt werden muß.
- Die letztmöglichen Ansagezeitpunkte sind je nach dem Zeitpunkt der Partnerschaftsklärung
variabel.
- Alle Ansagen erfolgen nach der Partnerschaftsklärung.
Hieraus folgt, daß der Zeitraum der Informationsübermittlung bezüglich des Treffens einer Ansage wesentlich größer sein kann. Das Essener System versucht nun Möglichkeiten aufzuzeigen wie der Zeitraum vor der Partnerschaftsklärung zur Informationsübermittlung ausgenutzt werden kann (vielfach durch konventionelle Anspiele) und welche zusätzlichen Möglichkeiten für das Ansageverhalten nach der Klärung der Partnerschaften bestehen. An Beispielen wird gezeigt wie leicht eine Optimierung des Spieles bei einer Hochzeit ist, wenn alle Möglichkeiten der Informationsübermittlung sinnvoll ausgenutzt werden. Ebenso werden wir auf einige Besonderheiten bei dem Ansageverhalten der KONTRA-Partei eingehen.
Partnerwahl
Grundlagen
Für die Partnerwahl bei der Hochzeit sind zwei Standpunkte zu berücksichtigen:
- Der (anspielende) Nichthochzeiter
- Der (anspielende) Hochzeiter.
1) Die Sichtweise des (anspielenden) Nichthochzeiters
Aus der Sicht des Nichthochzeiters sollte es oberstes Ziel sein der Partner des Hochzeiters zu werden. Eine Auswertung des Dodge-Einladungsturnieres München 92 hat gezeigt, daß circa 83% der Hochzeiten gewonnen wurden, während vergleichsweise die Siegquote für die REPartei bei den übrigen Normalspielen bei circa 66% lag. Ein absichtliches Verzichten auf die Heirat ist selbst mit guten Karten nicht sinnvoll:
- Der Spieler kann sich nicht sicher sein gegen die Hochzeit zu gewinnen, während er mit dem
Hochzeiter meistens gewinnt.
- Selbst wenn es zu einem RE/KONTRA-Spiel kommt (Wert » 6 Punkte + Sonderpunkte), hat
der Spieler wahrscheinlich nicht die optimale Punktausbeute erzielt, da der Hochzeiter
ebenfalls gute Karten gehabt haben dürfte und somit mit ihm eine höhere Punktausbeute möglich gewesen wäre (bei keine 60-Ansage = 7 Punkte + Sonder-punkte, die bei dem Zusammenspiel
zweier starker Blätter ebenfalls wahrscheinlicher sind).
Aus den bisherigen Argumenten folgt, daß der Nichthochzeiter das sicherste Anspiel wählen
sollte bzw. alle Mitspieler (inkl. des Hochzeiters) bei Fehlanspiel abstechen sollte. Das sicherste
Anspiel ist ![]() . Danach folgt das laufwahrscheinlichste As (kann auch Doppelas sein: vor
. Danach folgt das laufwahrscheinlichste As (kann auch Doppelas sein: vor ![]()
![]() sollte
sollte ![]()
![]() gespielt werden!). Wir persönlich halten das
gespielt werden!). Wir persönlich halten das ![]() -Anspiel nicht immer für gut.
Bei Besitz von guten Assen (schwarzes As mit maximal einer Nebenkarte) neben einer
-Anspiel nicht immer für gut.
Bei Besitz von guten Assen (schwarzes As mit maximal einer Nebenkarte) neben einer ![]() halten wir das Anspiel des Asses für sinnvoller, da das Anspiel der
halten wir das Anspiel des Asses für sinnvoller, da das Anspiel der ![]() ein Einbüßen der
Trumpfkontrolle zur Folge hat (hohe Trumpf der eigenen Partei sitzen nur noch bei einem
Spieler). Dies gilt besonders, wenn der Spieler gegenüber oder rechts vom Hochzeiter sitzt. Der Verlust bzw. die Einschränkung der Trumpfkontrolle kann von einer Verminderung der Punktausbeute bis hin zum Verlust des Spieles führen. Andererseits ist die Gefahr, daß der Spieler nicht Partner des Hochzeiters wird nur gering (» 17% bei As x). Mit den folgenden Blättern wäre das Anspiel eines Asses nach unserer Meinung besser:
(...)
ein Einbüßen der
Trumpfkontrolle zur Folge hat (hohe Trumpf der eigenen Partei sitzen nur noch bei einem
Spieler). Dies gilt besonders, wenn der Spieler gegenüber oder rechts vom Hochzeiter sitzt. Der Verlust bzw. die Einschränkung der Trumpfkontrolle kann von einer Verminderung der Punktausbeute bis hin zum Verlust des Spieles führen. Andererseits ist die Gefahr, daß der Spieler nicht Partner des Hochzeiters wird nur gering (» 17% bei As x). Mit den folgenden Blättern wäre das Anspiel eines Asses nach unserer Meinung besser:
(...)
2) Die Sichtweise des (anspielenden) Hochzeiters
Das Ziel des Hochzeiters bei der Partnerwahl sollte es sein, zunächst sein eigenes Blatt aufzuwerten,
da er kaum beurteilen kann, welcher seiner Mitspieler das beste Blatt besitzt. Dabei sollte
er zunächst versuchen eigene Asse zu spielen (auch ein angespieltes As abstechen) und dann
mit dem Anspiel den Partner suchen, welches sein eigenes Blatt am meisten aufwertet. Dabei
führt das Anspiel eines Trumpfes immer zu einer Aufwertung des eigenen Blattes, da auf jeden
Fall eine ![]() aus dem Spiel verschwindet (eventuell erwischt man sogar den Partner mit Doppel-
aus dem Spiel verschwindet (eventuell erwischt man sogar den Partner mit Doppel-
![]() ) und somit die eigenen hohen Trumpf (
) und somit die eigenen hohen Trumpf (![]() und
und ![]() ?) im weiteren Spiel eine dominierendere
Rolle spielen können. Zudem ist es wahrscheinlicher, daß der in Trumpf angespielte Partner
noch mindestens ein As besitzt, als daß der über Fehl angespielte Partner noch mindestens eine
?) im weiteren Spiel eine dominierendere
Rolle spielen können. Zudem ist es wahrscheinlicher, daß der in Trumpf angespielte Partner
noch mindestens ein As besitzt, als daß der über Fehl angespielte Partner noch mindestens eine
![]() besitzt. Dies heißt allerdings nicht, daß das Trumpfanspiel das beste Anspiel sein muß.
Trumpfanspiel erscheint nicht sinnvoll bei schwachen Blättern (i.d.R. gekennzeichnet durch
Trumpfkürze < 7), da man auf einen starken Partner angewiesen ist. Durch das Trumpfanspiel
verliert der Partner auf jeden Fall eine
besitzt. Dies heißt allerdings nicht, daß das Trumpfanspiel das beste Anspiel sein muß.
Trumpfanspiel erscheint nicht sinnvoll bei schwachen Blättern (i.d.R. gekennzeichnet durch
Trumpfkürze < 7), da man auf einen starken Partner angewiesen ist. Durch das Trumpfanspiel
verliert der Partner auf jeden Fall eine ![]() , was zu einer Schwächung seines Blattes führt. Die
Aufwertung des eigenen Blattes ist geringer zu bewerten als die potentielle Schwächung des
Partnerblattes. Fehlanspiel erscheint auch sinnvoll, wenn eine Aufwertung des eigenen
Trumpfblattes kaum möglich ist (bei z.B.
, was zu einer Schwächung seines Blattes führt. Die
Aufwertung des eigenen Blattes ist geringer zu bewerten als die potentielle Schwächung des
Partnerblattes. Fehlanspiel erscheint auch sinnvoll, wenn eine Aufwertung des eigenen
Trumpfblattes kaum möglich ist (bei z.B. ![]()
![]()
![]()
![]() ) bzw. der Fehlstich besonders wertvoll
werden kann oder die Farbe sehr lang ist. Hier hofft der Spieler den Partner zu finden, der diese
Farbe sticht und somit die weiteren Verlierer in der Farbe abdeckt. Diese Argumentation zeigt
schon, daß die Partnerwahl aus der Sicht des Hochzeiters sehr stark von der Struktur des
eigenen Blattes abhängt. Zur Verdeutlichung der Argumente für die einzelnen Anspiele daher
einige Beispielblätter: (...)
) bzw. der Fehlstich besonders wertvoll
werden kann oder die Farbe sehr lang ist. Hier hofft der Spieler den Partner zu finden, der diese
Farbe sticht und somit die weiteren Verlierer in der Farbe abdeckt. Diese Argumentation zeigt
schon, daß die Partnerwahl aus der Sicht des Hochzeiters sehr stark von der Struktur des
eigenen Blattes abhängt. Zur Verdeutlichung der Argumente für die einzelnen Anspiele daher
einige Beispielblätter: (...)
(Anspiel-)Konventionen
Wir unterscheiden zwischen (Anspiel-)Konventionen bei Anspiel einer der Nichthochzeiter und Anspiel des Hochzeiters. Allen Konventionen ist gemeinsam, daß sie eine klar umrissene Information enthalten, die für den betreffenden Spieler im Hinblick auf die Optimierung der Hochzeit eine große Bedeutung besitzen. Das Ziel der folgenden (Anspiel-)Konventionen ist dasselbe: Maximaler Informationsaustausch der Partnerschaft vor dem Zeitpunkt der Erstansage, um herauszufinden, ob in diesem Spiel eine hohe Punktzahl erzielt werden kann.
Konventionen des Nichthochzeiters
Hierzu gehören das Anspiel eines ![]() -Vollen und von
-Vollen und von ![]() , sowie der Abwurf einer Fehlkarte auf
ein angespieltes As des Hochzeiters:
, sowie der Abwurf einer Fehlkarte auf
ein angespieltes As des Hochzeiters:
Anspiel von KARO As/KARO 10
Bedeutung: Der Spieler ist im Besitz von Doppel-![]() und lang Trumpf (³8). Der Hochzeiter ist
verpflichtet den Stich zu nehmen und den Partner sofort durch Trumpfrückspiel zu suchen. Muß
der Hochzeiter den angespielten Karo-Vollen nicht mit
und lang Trumpf (³8). Der Hochzeiter ist
verpflichtet den Stich zu nehmen und den Partner sofort durch Trumpfrückspiel zu suchen. Muß
der Hochzeiter den angespielten Karo-Vollen nicht mit ![]() mitnehmen (er besitzt
mitnehmen (er besitzt ![]() oder er sitzt
rechts vom Anspielenden, wobei ihm kein zu hoher Trumpf vorgelegt wird) kann er seinerseits
Trumpflänge zeigen, indem er mit ³ 7 Trumpf zunächst
oder er sitzt
rechts vom Anspielenden, wobei ihm kein zu hoher Trumpf vorgelegt wird) kann er seinerseits
Trumpflänge zeigen, indem er mit ³ 7 Trumpf zunächst ![]() (wenn möglich
(wenn möglich ![]() ) nachspielt, bevor
er klein Trumpf zurückspielt. Links vom Anspielenden sitzend kann er zusätzlich auch durch einen
Schnitt (z.B. mit
) nachspielt, bevor
er klein Trumpf zurückspielt. Links vom Anspielenden sitzend kann er zusätzlich auch durch einen
Schnitt (z.B. mit ![]() oder
oder ![]() ) seine Trumpflänge zeigen. Bei fehlender Trumpflänge verzichtet
er auf das mögliche Vorspiel einer
) seine Trumpflänge zeigen. Bei fehlender Trumpflänge verzichtet
er auf das mögliche Vorspiel einer ![]() /
/![]() . Besitzt der anspielende Nichthochzeiter die
Kombination Doppel-
. Besitzt der anspielende Nichthochzeiter die
Kombination Doppel-![]() + Karo-Vollen ohne die angegebene Gesamttrumpfzahl so zeigt er
dies, indem er zunächst sich mit
+ Karo-Vollen ohne die angegebene Gesamttrumpfzahl so zeigt er
dies, indem er zunächst sich mit ![]() in die Hochzeit einklinkt und dann gegebenenfalls den
Karo-Vollen folgen läßt. Das Ziel dieser Konvention ist es, schon vor dem eigentlichen Zeitpunkt
einer Erstansage wichtige Informationen über Trumpfstärke und Trumpflänge auszutauschen
und somit schon sehr früh einen Überblick über die Anzahl der Trumpfverlierer zu erhalten. Diese
Konvention ist logisch einwandfrei, da es für einen Spieler ohne Doppel-
in die Hochzeit einklinkt und dann gegebenenfalls den
Karo-Vollen folgen läßt. Das Ziel dieser Konvention ist es, schon vor dem eigentlichen Zeitpunkt
einer Erstansage wichtige Informationen über Trumpfstärke und Trumpflänge auszutauschen
und somit schon sehr früh einen Überblick über die Anzahl der Trumpfverlierer zu erhalten. Diese
Konvention ist logisch einwandfrei, da es für einen Spieler ohne Doppel-![]() überhaupt keinen
Sinn ergibt einen Karo-Vollen vorzuspielen, da ein möglicher Zusammenfall von
überhaupt keinen
Sinn ergibt einen Karo-Vollen vorzuspielen, da ein möglicher Zusammenfall von ![]() und
und ![]() in
einem Stich bis auf eine mögliche Verteilung ausgeschlossen ist: Nur bei einem Hochzeiter links
vom anspielenden Spieler ohne
in
einem Stich bis auf eine mögliche Verteilung ausgeschlossen ist: Nur bei einem Hochzeiter links
vom anspielenden Spieler ohne ![]() (mit
(mit ![]() würde er nicht
würde er nicht ![]() legen) und verteilten
legen) und verteilten ![]() en (bei Doppel-
en (bei Doppel-![]() wird keine
wird keine ![]() gelegt, da eh Trumpf zurück gespielt wird) bei den anderen beiden
Spielern kann dieser Fall eintreten. Die Wahrscheinlichkeit hierfür beträgt circa 25%. Eine
Erweiterung dieser Konvention auf jegliches Trumpfanspiel eines Nichthochzeiters erscheint nicht
sinnvoll, da einem Nichthochzeiter ohne Einklinkmöglichkeit nicht die Option genommen werden
soll, Trumpf auszuspielen, um sein eigenes Trumpfblatt aufzuwerten bzw. die Gewinnaussichten
gegen die Hochzeit zu erhöhen. Beispielblatt:
gelegt, da eh Trumpf zurück gespielt wird) bei den anderen beiden
Spielern kann dieser Fall eintreten. Die Wahrscheinlichkeit hierfür beträgt circa 25%. Eine
Erweiterung dieser Konvention auf jegliches Trumpfanspiel eines Nichthochzeiters erscheint nicht
sinnvoll, da einem Nichthochzeiter ohne Einklinkmöglichkeit nicht die Option genommen werden
soll, Trumpf auszuspielen, um sein eigenes Trumpfblatt aufzuwerten bzw. die Gewinnaussichten
gegen die Hochzeit zu erhöhen. Beispielblatt: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Das
Anspiel von Trumpf erscheint sinnvoll, sofern der Spieler nicht rechts vom Hochzeiter sitzt. In
diesem Fall könnte er noch darauf hoffen, daß der Hochzeiter sowohl ein laufendes
Das
Anspiel von Trumpf erscheint sinnvoll, sofern der Spieler nicht rechts vom Hochzeiter sitzt. In
diesem Fall könnte er noch darauf hoffen, daß der Hochzeiter sowohl ein laufendes ![]() und
und ![]() (...)
(...)
Anspiel von Pik-Dame
Bedeutung: Der Spieler ist im Besitz von Doppel-![]() , die Trumpflänge ist nicht festgelegt. Besitzt
der Spieler jedoch noch einen Karo-Vollen, so sollte er mit eigener Trumpflänge auf das
Vorspiel der
, die Trumpflänge ist nicht festgelegt. Besitzt
der Spieler jedoch noch einen Karo-Vollen, so sollte er mit eigener Trumpflänge auf das
Vorspiel der ![]() verzichten, da er sonst auf eine Trumpfrunde vor der Erstansage verzichtet und
verzichten, da er sonst auf eine Trumpfrunde vor der Erstansage verzichtet und
![]() beim Rückspiel des Hochzeiters immer noch zeigen kann. Der Vorteil, daß der Hochzeiter
eventuell schon
beim Rückspiel des Hochzeiters immer noch zeigen kann. Der Vorteil, daß der Hochzeiter
eventuell schon ![]() (bei Besitz der anderen
(bei Besitz der anderen ![]() ) auf das nächste Trumpfanspiel legen kann ist
nicht ausreichend. Ohne Trumpflänge sollte er analog der ersten (Anspiel-)Konvention mit
) auf das nächste Trumpfanspiel legen kann ist
nicht ausreichend. Ohne Trumpflänge sollte er analog der ersten (Anspiel-)Konvention mit ![]() beginnen. Das Anspiel einer
beginnen. Das Anspiel einer ![]() ohne den Besitz von Doppel-
ohne den Besitz von Doppel-![]() ist aus den gleichen Überlegungen
wie bei der vorherigen (Anspiel-)Konvention logisch nicht nachvollziehbar.
ist aus den gleichen Überlegungen
wie bei der vorherigen (Anspiel-)Konvention logisch nicht nachvollziehbar.
Abwurf auf ein angespieltes Fehlas des Hochzeiters
Bedeutung: Dies kennzeichnet i.d.R. ein Singleton in der abgeworfenen Farbe (links vom Hochzeiter
sitzend wird auch von As x abgeworfen) und Trumpflänge (³ 8). Der Abwurf sagt bei einem
Abwurf einer Karte in einer der schwarzen Farben nichts über den Besitz von ![]() en aus. Auf
den Abwurf von HERZ-Singleton wird häufig verzichtet, da der Vorteil des HERZ-Stechens dem Risiko,
daß der Spieler nicht Partner des Hochzeiters wird, nicht ausgleicht. Der Abwurf eines HERZ-
Singletons erfolgt nur dann, wenn der Spieler über Trumpf angespielt werden kann, d.h. er besitzt
links vom Hochzeiter sitzend eine
en aus. Auf
den Abwurf von HERZ-Singleton wird häufig verzichtet, da der Vorteil des HERZ-Stechens dem Risiko,
daß der Spieler nicht Partner des Hochzeiters wird, nicht ausgleicht. Der Abwurf eines HERZ-
Singletons erfolgt nur dann, wenn der Spieler über Trumpf angespielt werden kann, d.h. er besitzt
links vom Hochzeiter sitzend eine ![]() , ansonsten Doppel-
, ansonsten Doppel-![]() . Gleiches gilt übrigens auch
bei dem Abwurf einer Standkarte (= As) Warum? Bei Abwurf eines HERZ-Singletons ist die Gefahr,
daß der abwerfende Spieler überstochen wird wesentlich höher als bei dem Abwurf eines
schwarzen Singletons: Im ersten Fall sind in beiden Farben maximal noch 5 Karten bei den anderen
Spielern, während im zweiten Fall maximal noch 5 (bei Anspiel von
. Gleiches gilt übrigens auch
bei dem Abwurf einer Standkarte (= As) Warum? Bei Abwurf eines HERZ-Singletons ist die Gefahr,
daß der abwerfende Spieler überstochen wird wesentlich höher als bei dem Abwurf eines
schwarzen Singletons: Im ersten Fall sind in beiden Farben maximal noch 5 Karten bei den anderen
Spielern, während im zweiten Fall maximal noch 5 (bei Anspiel von ![]() 3) in der einen
Farbe und 7 der abgeworfenen Farbe bei den anderen Spielern. Der Abwurf einer Standkarte ist
nicht unbedingt notwendig, aus diesem Grund erscheint es logisch dies nur zu unternehmen,
wenn der Spieler dennoch sicher Partner des Hochzeiters werden kann. Der Hochzeiter ist bei
Abwurf eines schwarzen Singletons verpflichtet, die bessere der beiden Farben (= Farbe, in denen
die übrigen beiden Spieler die meisten Karten halten), die der abwerfende Spieler nicht mehr
besitzt, nachzuspielen. Er kann zunächst auch noch eine
3) in der einen
Farbe und 7 der abgeworfenen Farbe bei den anderen Spielern. Der Abwurf einer Standkarte ist
nicht unbedingt notwendig, aus diesem Grund erscheint es logisch dies nur zu unternehmen,
wenn der Spieler dennoch sicher Partner des Hochzeiters werden kann. Der Hochzeiter ist bei
Abwurf eines schwarzen Singletons verpflichtet, die bessere der beiden Farben (= Farbe, in denen
die übrigen beiden Spieler die meisten Karten halten), die der abwerfende Spieler nicht mehr
besitzt, nachzuspielen. Er kann zunächst auch noch eine ![]() vorspielen. Dies zeigt Trumpflänge
(³ 7) und fragt nach der anderen
vorspielen. Dies zeigt Trumpflänge
(³ 7) und fragt nach der anderen ![]() . Der Spieler zeigt sie, indem er einen Karo-Vollen schmiert.
Es folgt dann Trumpfnachspiel. Der Umkehrschluß keinen Karo-Vollen = keine
. Der Spieler zeigt sie, indem er einen Karo-Vollen schmiert.
Es folgt dann Trumpfnachspiel. Der Umkehrschluß keinen Karo-Vollen = keine ![]() ist natürlich
nicht gültig. Das Nachspiel von
ist natürlich
nicht gültig. Das Nachspiel von ![]() kann zur Deklaration der eigenen Trumpflänge und
Verschiebung des Ansagezeitpunktes auch bei Abwurf eines HERZ-Singletons erfolgen. Sicherlich ist
Dir auch die von anderen Doppelkopfexperten verwendete Konvention, daß ein Abwurf auf ein
angespieltes As des Hochzeiters immer Doppel-
kann zur Deklaration der eigenen Trumpflänge und
Verschiebung des Ansagezeitpunktes auch bei Abwurf eines HERZ-Singletons erfolgen. Sicherlich ist
Dir auch die von anderen Doppelkopfexperten verwendete Konvention, daß ein Abwurf auf ein
angespieltes As des Hochzeiters immer Doppel-![]() deklariert und nichts über die abgeworfene
Farbe und der Trumpflänge aussagt, bekannt. Wir sind der Meinung, daß die wesentliche
größere Anwendungswahrscheinlichkeit unserer Konvention inklusive des höheren
Informationsgehaltes den Vorteil, daß bei der anderen Konvention der Abwurf ohne Risiko geschieht,
überwiegt.
deklariert und nichts über die abgeworfene
Farbe und der Trumpflänge aussagt, bekannt. Wir sind der Meinung, daß die wesentliche
größere Anwendungswahrscheinlichkeit unserer Konvention inklusive des höheren
Informationsgehaltes den Vorteil, daß bei der anderen Konvention der Abwurf ohne Risiko geschieht,
überwiegt.
Konventionen des Hochzeiters
Anspiel von Herz-10 zum 1.Stich
Bedeutung: Der Hochzeiter besitzt Trumpflänge (³ 8) und zeigt damit, daß er den Partner über
Trumpf suchen wird. Er kann im 2.Stich zur Information seines Partners noch ![]() folgen lassen,
allerdings darf er kein Fehlas spielen, da dies von einem anderen Spieler als demjenigen mit der
anderen
folgen lassen,
allerdings darf er kein Fehlas spielen, da dies von einem anderen Spieler als demjenigen mit der
anderen ![]() abgestochen werden könnte. Will der Hochzeiter zunächst ein As spielen, so kann
er die verwandte (Anspiel-)Konvention 2 (siehe unten) anwenden. Die Idee dieser Variante ist
neben der mitgeteilten Information über das eigene Blatt und der Verschiebung des Ansagezeitpunktes
nach hinten auch durch die gelegte Karte des Partners auf den angespielten kleinen
Trumpf zum eigentlichen Klärungsstich Informationen über dessen Blatt zu erhalten: Er sollte mit
abgestochen werden könnte. Will der Hochzeiter zunächst ein As spielen, so kann
er die verwandte (Anspiel-)Konvention 2 (siehe unten) anwenden. Die Idee dieser Variante ist
neben der mitgeteilten Information über das eigene Blatt und der Verschiebung des Ansagezeitpunktes
nach hinten auch durch die gelegte Karte des Partners auf den angespielten kleinen
Trumpf zum eigentlichen Klärungsstich Informationen über dessen Blatt zu erhalten: Er sollte mit
![]()
![]() die
die ![]() legen bzw. mit
legen bzw. mit ![]()
![]()
![]() bei zusätzlichem Nachspiel des Hochzeiters von
bei zusätzlichem Nachspiel des Hochzeiters von ![]() die
die ![]() legen, sofern ihm die gleiche Karte nicht vorgelegt wird oder er rechts vom Hochzeiter
sitzend auch mit einer anderen Karte den Klärungsstich gewinnen kann. Spielt der Hochzeiter
nach der
legen, sofern ihm die gleiche Karte nicht vorgelegt wird oder er rechts vom Hochzeiter
sitzend auch mit einer anderen Karte den Klärungsstich gewinnen kann. Spielt der Hochzeiter
nach der ![]() noch
noch ![]() nach so zeigt er ein extrem starkes Blatt (Minimum 9 gute Trumpf mit
maximal einem Fehlabgeber).
nach so zeigt er ein extrem starkes Blatt (Minimum 9 gute Trumpf mit
maximal einem Fehlabgeber).
Anspiel von Herz-10 oder Pik-Dame zum 2.Stich
Bedeutung: Der Hochzeiter besitzt Trumpflänge (³ 8) und im ersten Fall keine ![]() zu seiner
zu seiner ![]() und im zweiten Fall eine
und im zweiten Fall eine ![]() zu seiner
zu seiner ![]() . Diese (Anspiel-)Konvention hat die gleiche Idee wie
die vorherige Variante und die gleiche Konsequenz für die Partnerwahl. Sie wird angewendet
zum einen, wenn der Hochzeiter es vorzieht zum ersten Stich ein As zu spielen, oder zum anderen,
wenn der Hochzeiter zum ersten Stich kein Anspiel besaß. Aus dieser Beschreibung folgt
auch, daß der Hochzeiter mit eigenem Anspiel zum ersten Stich bei Verwendung der (Anspiel-)-
Konvention 1 i.d.R. kein gutes Anspielas besitzt. Das Anspiel der
. Diese (Anspiel-)Konvention hat die gleiche Idee wie
die vorherige Variante und die gleiche Konsequenz für die Partnerwahl. Sie wird angewendet
zum einen, wenn der Hochzeiter es vorzieht zum ersten Stich ein As zu spielen, oder zum anderen,
wenn der Hochzeiter zum ersten Stich kein Anspiel besaß. Aus dieser Beschreibung folgt
auch, daß der Hochzeiter mit eigenem Anspiel zum ersten Stich bei Verwendung der (Anspiel-)-
Konvention 1 i.d.R. kein gutes Anspielas besitzt. Das Anspiel der ![]() kann in unseren Augen
keinen Versuch darstellen mit einer
kann in unseren Augen
keinen Versuch darstellen mit einer ![]() nachträglich ein Karo-Solo spielen zu wollen, da die
Punktausbeute bei dem Solo nur in seltenen Fällen (Der Spieler muß die 90 sicher ansagen
können) höher sein wird als bei der Hochzeit mit dem Partner mit der anderen
nachträglich ein Karo-Solo spielen zu wollen, da die
Punktausbeute bei dem Solo nur in seltenen Fällen (Der Spieler muß die 90 sicher ansagen
können) höher sein wird als bei der Hochzeit mit dem Partner mit der anderen ![]() .
.
Anspiel von Kreuz-Dame zum 1. oder 2.Stich
(ohne vorheriges Anspiel der ![]() )
)
Bedeutung: Der Hochzeiter besitzt Doppel-![]() und zumeist Trumpflänge und wird seinen Partner
über Trumpf suchen. Wie bei der (Anspiel-)Konvention 1 kann er noch zusätzlich eine
und zumeist Trumpflänge und wird seinen Partner
über Trumpf suchen. Wie bei der (Anspiel-)Konvention 1 kann er noch zusätzlich eine ![]() folgen lassen. Ein extrem starkes Blatt (Minimum 9 Trumpf mit ...) kann er analog zur (Anspiel-)-
Konvention 2 durch Nachspiel der zweiten
folgen lassen. Ein extrem starkes Blatt (Minimum 9 Trumpf mit ...) kann er analog zur (Anspiel-)-
Konvention 2 durch Nachspiel der zweiten ![]() deklarieren.
Bei allen diesen (Anspiel-)Konventionen ist keine spezifische Reaktion des zukünftigen Partners
auf das jeweilige Anspiel vorgesehen. Eine Übermittlung der eigenen Trumpflänge ist nur bedingt
möglich, da bei dem Fehlen einer Trumpflänge keine allzu große Auswahl besteht. Vereinbarungsgemäß
kann versucht werden durch die Reihenfolge der ersten beiden freiwillig (der
Trumpf im Klärungsstich ist ausgenommen!) bedienten Trumpf Trumpflänge zu zeigen oder zu
verneinen. Ein Niedrig-Hoch-Signal (1. Trumpf niedriger oder gleich 2.Trumpf) bedeutet Trumpfkürze
(< 7), während ein Hoch-Niedrig-Signal (1.Trumpf höher als 2.Trumpf) Trumpflänge (³ 7)
deklariert. Diese Übereinkunft ist besonders wirksam, bei den (Anspiel-)Konventionen, bei denen
der Hochzeiter zwei Trumpf von oben spielt. Im anderen Fall ist sie allerdings ebenfalls anwendbar,
nur muß sich der Hochzeiter den zuerst gelegten Trumpf seines Partners eventuell
längere Zeit merken. Diese Vereinbarung erscheint sinnvoll, da der Hochzeiter bei der Anwendung
der (Anspiel-)Konventionen keine vorzeitige Information über die Sitzposition seines Partners
benötigt.
Auf Beispielblätter zu den einzelnen (Anspiel-)Konventionen können wir aufgrund der klar umrissenen
Blattstrukturen für die einzelnen Varianten verzichten.
deklarieren.
Bei allen diesen (Anspiel-)Konventionen ist keine spezifische Reaktion des zukünftigen Partners
auf das jeweilige Anspiel vorgesehen. Eine Übermittlung der eigenen Trumpflänge ist nur bedingt
möglich, da bei dem Fehlen einer Trumpflänge keine allzu große Auswahl besteht. Vereinbarungsgemäß
kann versucht werden durch die Reihenfolge der ersten beiden freiwillig (der
Trumpf im Klärungsstich ist ausgenommen!) bedienten Trumpf Trumpflänge zu zeigen oder zu
verneinen. Ein Niedrig-Hoch-Signal (1. Trumpf niedriger oder gleich 2.Trumpf) bedeutet Trumpfkürze
(< 7), während ein Hoch-Niedrig-Signal (1.Trumpf höher als 2.Trumpf) Trumpflänge (³ 7)
deklariert. Diese Übereinkunft ist besonders wirksam, bei den (Anspiel-)Konventionen, bei denen
der Hochzeiter zwei Trumpf von oben spielt. Im anderen Fall ist sie allerdings ebenfalls anwendbar,
nur muß sich der Hochzeiter den zuerst gelegten Trumpf seines Partners eventuell
längere Zeit merken. Diese Vereinbarung erscheint sinnvoll, da der Hochzeiter bei der Anwendung
der (Anspiel-)Konventionen keine vorzeitige Information über die Sitzposition seines Partners
benötigt.
Auf Beispielblätter zu den einzelnen (Anspiel-)Konventionen können wir aufgrund der klar umrissenen
Blattstrukturen für die einzelnen Varianten verzichten.
Ansageverhalten der RE-Partei
Grundlagen
Alle Ansagen beider Parteien erfolgen bei geklärten Partnerschaftsverhältnissen. Es gelten die gleichen Prinzipien wie bei der Optimierung (Ausreizen) des Normalspieles. Das wichtigste sei an dieser Stelle nochmals wiederholt: Bei gleichem Informationsstand über das Spiel wird eine Ansage, die sich nur auf diesen Informationsstand bezieht immer von dem im für diese Ansage entscheidenden Stich weiter hintensitzenden Partner vorgenommen. Eine verfrühte Ansage deklariert immer Zusatzwerte, deren Größenordnung von der jeweiligen Situation abhängt. Die Wiederholung dieses Grundprinzips für Ansagen bei geklärter Partnerschaft erscheint hier sinnvoll, da gerade bei der Hochzeit häufig ein höherer beiderseitiger Informationsstand über das Spiel im Vergleich zum Normalspiel vorliegt. Für die Hilfsmittel des Essener Systems (Ansagen, Ansagezeitpunkte, Anfragen bei geklärter Partnerschaft) gelten die gleichen Prinzipien wie bei der Optimierung (Ausreizen) des Normalspieles dargestellt: Eine vorzeitige Ansage mit einer Karte dient als Kommentar zur Karte oder Farbe. Eine Ansage vor dem Anspiel des Partners will diesen vom Normalanspiel abbringen oder auch freiwillig den Besitz bestimmter Karten anzeigen. Eine Anfrage dient immer dazu herauszufinden, ob der Partner eine bestimmte Karte besitzt oder nicht besitzt. Bei den Normalspielen kamen diese Hilfsmittel i.d.R. erst bei weiteren Ansagen zum Tragen. Bei der Hochzeit können sie allerdings analog der Bedeutung im Kapitel Optimieren (Ausreizen) des Normalspieles schon für das Treffen der Erstansage angewendet werden. Da dies bei den Normalspielen nicht so ist, haben wir im folgenden einige spezifische Beispiele der Anwendung und Bedeutung im Hinblick auf die Erstansage für die Hochzeit zusammengestellt:
Erstansage des Hochzeiters (freiwillige) vor Anspiel des Partners
Die Bedeutung hängt von der Sitzposition des Hochzeiters zu seinem Partner und der Art des
Einklinkens des Nichthochzeiters ab. Wir unterscheiden drei Einklinkmöglichkeiten (![]() ,
schwarzes As und
,
schwarzes As und ![]() ) und drei Sitzkombinationen (rechts, gegenüber und links vom Hochzeiter):
) und drei Sitzkombinationen (rechts, gegenüber und links vom Hochzeiter):
Einklinken mit ![]() Bedeutung: Der Hochzeiter besitzt unabhängig von der Sitzposition die andere
Bedeutung: Der Hochzeiter besitzt unabhängig von der Sitzposition die andere ![]() und ein Blatt
mit dem er Gewinnaussichten von mehr als 50% sieht (bei knapp durchschnittlichem Blatt des
Partners). Sitzt der Partner rechts vom Hochzeiter, so besitzt der Hochzeiter i.d.R. nur Erstrundenkontrolle
(hier = As) in einer der schwarzen Farben. Er will verhindern, daß der Partner ihn
in der falschen Farbe anschiebt, daher ist hier diese Erstansage auch mit einem etwas
schwächeren Blatt erlaubt. Der Partner ist bei keiner Sitzposition verpflichtet, Trumpf zu spielen,
d.h. er kann zunächst eigene Asse spielen. Mit sehr starken Blättern kann der Hochzeiter auch
sofort RE und keine 90 ansagen. Er fordert damit zwingend Trumpfanspiel und sollte diese Ansage
aber auch mit Minimum des Partners verantworten können.
und ein Blatt
mit dem er Gewinnaussichten von mehr als 50% sieht (bei knapp durchschnittlichem Blatt des
Partners). Sitzt der Partner rechts vom Hochzeiter, so besitzt der Hochzeiter i.d.R. nur Erstrundenkontrolle
(hier = As) in einer der schwarzen Farben. Er will verhindern, daß der Partner ihn
in der falschen Farbe anschiebt, daher ist hier diese Erstansage auch mit einem etwas
schwächeren Blatt erlaubt. Der Partner ist bei keiner Sitzposition verpflichtet, Trumpf zu spielen,
d.h. er kann zunächst eigene Asse spielen. Mit sehr starken Blättern kann der Hochzeiter auch
sofort RE und keine 90 ansagen. Er fordert damit zwingend Trumpfanspiel und sollte diese Ansage
aber auch mit Minimum des Partners verantworten können.
(...) Einklinken mit einem schwarzen As
1) Partner sitzt rechts vom Hochzeiter
Bedeutung: Abbringen vom Normalanspiel. Das normale Anspiel wäre, wenn kein weiteres As
mehr vorhanden ist (nur der Fall ist interessant), ein Anschieben in der anderen schwarzen Farbe.
Dies soll mit der Ansage verhindert werden, d.h. der Hochzeiter besitzt lediglich ![]() . Die
Stärke des Blattes des Hochzeiters sollte gleich der bei einer Erstansage nach angespielter
. Die
Stärke des Blattes des Hochzeiters sollte gleich der bei einer Erstansage nach angespielter ![]() an dieser Position sein, z.B.:
an dieser Position sein, z.B.: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Diese Erstansage
macht keine Aussage über
. Diese Erstansage
macht keine Aussage über ![]() en. Der Partner spielt möglicherweise zunächst noch das andere
schwarze As und dann HERZ unter. Besitzt er selbst
en. Der Partner spielt möglicherweise zunächst noch das andere
schwarze As und dann HERZ unter. Besitzt er selbst ![]() oder ist Chicane in der Farbe kann er auch
Trumpf nachspielen.
oder ist Chicane in der Farbe kann er auch
Trumpf nachspielen.
2) Partner sitzt gegenüber vom Hochzeiter
Die vorzeitige freiwillige RE-Ansage zeigt ein starkes RE-Blatt, d.h Trumpflänge (³ 8) und
Trumpfhöhe (inkl. einer ![]() ). Der Partner sollte nur noch gute Asse (schwarzes As mit maximal
zwei Nebenkarten oder
). Der Partner sollte nur noch gute Asse (schwarzes As mit maximal
zwei Nebenkarten oder ![]() ohne Nebenkarte) spielen, alternativ Trumpf. Diese Interpretation
der Ansage erscheint logisch, da das Normalanspiel nach Abspiel der restlichen Asse ohnehin
Trumpf gewesen wäre, und das Fordern des Nachspiels der Farbe des ersten Asses an dieser
Position nicht sinnvoll erscheint. Das Risiko des Überstechens kompensiert nicht die Erstansage.
Ein mögliches Blatt des Hochzeiters:
ohne Nebenkarte) spielen, alternativ Trumpf. Diese Interpretation
der Ansage erscheint logisch, da das Normalanspiel nach Abspiel der restlichen Asse ohnehin
Trumpf gewesen wäre, und das Fordern des Nachspiels der Farbe des ersten Asses an dieser
Position nicht sinnvoll erscheint. Das Risiko des Überstechens kompensiert nicht die Erstansage.
Ein mögliches Blatt des Hochzeiters: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
3) Partner sitzt links vom Hochzeiter
Hochzeiter besitzt Singleton in der Farbe des vorher angespielten Asses und wünscht das
Nachspiel der Farbe, da er weitere Asse (mindestens das andere schwarze As) besitzt, allerdings
über Trumpf nicht sicher angespielt werden kann. Die Erstansage dient dem Abbringen vom
Normalanspiel (Trumpf). Die Deutung der Erstansage erscheint an dieser Position logisch, da
keine Gefahr des Überstechens bei einem Nachspiel der Farbe besteht. Ein Vorstechen eines
Gegners mit einer
.
3) Partner sitzt links vom Hochzeiter
Hochzeiter besitzt Singleton in der Farbe des vorher angespielten Asses und wünscht das
Nachspiel der Farbe, da er weitere Asse (mindestens das andere schwarze As) besitzt, allerdings
über Trumpf nicht sicher angespielt werden kann. Die Erstansage dient dem Abbringen vom
Normalanspiel (Trumpf). Die Deutung der Erstansage erscheint an dieser Position logisch, da
keine Gefahr des Überstechens bei einem Nachspiel der Farbe besteht. Ein Vorstechen eines
Gegners mit einer ![]() wird durch den Abwurf und der Aufwertung des eigenen Trumpfblattes
kompensiert. Einzig unangenehm ist, wenn der Partner ein singleton As angespielt hat. Aus
diesem Grund sollte das Blatt des Hochzeiters nicht zu schwach sein. Beispielblatt:
wird durch den Abwurf und der Aufwertung des eigenen Trumpfblattes
kompensiert. Einzig unangenehm ist, wenn der Partner ein singleton As angespielt hat. Aus
diesem Grund sollte das Blatt des Hochzeiters nicht zu schwach sein. Beispielblatt: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
Stärkere Blätter, die immer ein sofortiges Trumpfanspiel fordern werden in allen drei Sitzpositionen
durch RE plus keine 90-Ansage deklariert. Der Spieler sollte mindestens eine
.
Stärkere Blätter, die immer ein sofortiges Trumpfanspiel fordern werden in allen drei Sitzpositionen
durch RE plus keine 90-Ansage deklariert. Der Spieler sollte mindestens eine ![]() und darf
keinen Fehlverlierer mehr besitzen (bei Doppel-
und darf
keinen Fehlverlierer mehr besitzen (bei Doppel-![]() sind auch Einzelasse keine Fehlverlierer). Er
garantiert die benötigte Sicherheit für diese Ansage auch bei einem schwachen Blatt seines
Partners.
sind auch Einzelasse keine Fehlverlierer). Er
garantiert die benötigte Sicherheit für diese Ansage auch bei einem schwachen Blatt seines
Partners.
3) Einklinken mit Herz-As
Sitzt der Hochzeiter links von seinem Partner zeigt die vorzeitige Ansage analog dem Einklinken
mit der ![]() an dieser Position mindestens eine
an dieser Position mindestens eine ![]() plus i.d.R. ein schwarzes As. Der Partner
weiß ja wiederum nicht in welcher der beiden schwarzen Farben er den Hochzeiter anspielen
kann. Es gelten die gleichen Konsequenzen für den Partner.
An den beiden übrigen Sitzpositionen ist die Erstansage aus den gleichen Überlegungen wie bei
Einklinken mit einem schwarzen As und Partner sitzt links vom Hochzeiter ein Zeichen für ein
starkes Blatt.
Bisher wurde lediglich das Ansageverhalten (Erstansage) bei normalem Einklinken in die Hochzeit
betrachtet. Bei den (Anspiel-)Konventionen sieht die Sachlage etwas anders aus. Bei
(Anspiel-)Konventionen ist sichergestellt, daß die eigene Partei zumindest die vier höchsten
Trumpf besitzt, zusätzlich können schon Informationen über die Trumpflänge eines oder beider
Partner vor dem Zeitpunkt der Erstansage vorliegen. Aus diesem Grund wird im Regelfall nach
Klärung der Partnerschaften zunächst die Anzahl der Fehlverlierer überprüft, d.h. es werden
Asse gespielt. Eine Erstansage vor dem Anspiel nach dem Klärungsstich fordert daher Trumpfnachspiel.
Grundlage hierfür sind Blätter ohne Fehlverlierer (As As x (x) ist kein Verlierer, auch
darf
plus i.d.R. ein schwarzes As. Der Partner
weiß ja wiederum nicht in welcher der beiden schwarzen Farben er den Hochzeiter anspielen
kann. Es gelten die gleichen Konsequenzen für den Partner.
An den beiden übrigen Sitzpositionen ist die Erstansage aus den gleichen Überlegungen wie bei
Einklinken mit einem schwarzen As und Partner sitzt links vom Hochzeiter ein Zeichen für ein
starkes Blatt.
Bisher wurde lediglich das Ansageverhalten (Erstansage) bei normalem Einklinken in die Hochzeit
betrachtet. Bei den (Anspiel-)Konventionen sieht die Sachlage etwas anders aus. Bei
(Anspiel-)Konventionen ist sichergestellt, daß die eigene Partei zumindest die vier höchsten
Trumpf besitzt, zusätzlich können schon Informationen über die Trumpflänge eines oder beider
Partner vor dem Zeitpunkt der Erstansage vorliegen. Aus diesem Grund wird im Regelfall nach
Klärung der Partnerschaften zunächst die Anzahl der Fehlverlierer überprüft, d.h. es werden
Asse gespielt. Eine Erstansage vor dem Anspiel nach dem Klärungsstich fordert daher Trumpfnachspiel.
Grundlage hierfür sind Blätter ohne Fehlverlierer (As As x (x) ist kein Verlierer, auch
darf ![]() x (x) vorhanden sein).
x (x) vorhanden sein).
Anfragen des Partners an den Hochzeiter direkt nach dem Klärungsstich
Die Bedeutung der Anfrage hängt wiederum von der Art des Einklinkens und der Sitzposition der
Partner zueinander ab. Es werden die gleichen Fälle wie bei der freiwilligen vorzeitigen Ansage
des Hochzeiters unterschieden. Es wird in allen Fällen nach bestimmten Karten beim Hochzeiter
gefragt. Alle Anfragen werden zumindest stark einladend gespielt, d. h. der Hochzeiter darf nur
mit einem sehr schwachen Blatt die Antwort verweigern, wenn er die besagte Karte hält. Auf eine
ausführliche Darstellung zu diesem Themenkomplex können wir verzichten, da alle Anfragen des
Partners sich auf die gleichen Karten beziehen, auf die der Hochzeiter unter Punkt 1) Erstansage
(freiwillige) vor Anspiel des Partners bei der jeweiligen Situation (Einklinkstich und Sitzposition)
eine freiwillige Ansage getätigt hat. Der Unterschied besteht nur darin, daß im Falle der Anfrage der Partner des Hochzeiters die Verantwortung für die Erstansage übernimmt und nicht der Hochzeiter selbst. Dies bedeutet beispielsweise: Bei Einklinken mit der ![]() (und auch mit
(und auch mit ![]() rechts vom Hochzeiter sitzend) eine Anfrage des Partner an den Hochzeiter nach einer
rechts vom Hochzeiter sitzend) eine Anfrage des Partner an den Hochzeiter nach einer ![]() .
.
(...)
Optimierung (Ausreizen) der Hochzeit
Die Grundlage für die Optimierung ist die systemgerechte Anwendung der Partnerwahl und der Erstansage. Hierauf aufbauend erfolgt das Ausreizen nach den gleichen Grundsätzen wie bei der Optimierung eines Normalspieles, die daher an dieser Stelle nicht nochmals wiederholt werden sollen (siehe Kap. 2.2.3). Ebenso werden die gleichen Hilfsmittel mit den analogen Bedeutungen auch hier eingesetzt. Hierbei muß nur beachtet werden, daß eine Klärung der Partnerschaft schon erfolgt ist. Also fallen beispielsweise vorzeitige Ansagen oder Anfragen zur Klärung der Partnerschaften weg. Wir haben dieses Kapitel hier aufgeführt, um zum einen zu zeigen, daß bei der Hochzeit ein sicheres Ausreizen des Spieles noch wesentlich einfacher als beim Normalspiel vonstatten geht, und zum anderen um einige Möglichkeiten, die im Kapitel Ansageverhalten neu sind, zu vertiefen. Es gelten die gleichen Randbedingungen wie im Kapitel 2.2.4 (...)
3.4 Ansageverhalten der KONTRA-Partei Die Problematik des Ansageverhaltens der KONTRA-Partei bei einer Hochzeit wird schnell offensichtlich, wenn man sich die Grundvorausetzungen für eine Erstansage (Kap. 2.1.1) oder auch Gegenansage (Kap. 2.3.1) in Erinnerung ruft und zusätzlich bedenkt, daß hier erschwerend hinzukommt, daß die Ansage gegen mindestens einen Stich und das Anspiel der RE-Partei gemacht wird. Dies zeigt schon, daß i.d.R. ein außerordentlich starkes Blatt vorhanden sein muß für eine Erstansage oder für eine Gegenansage auf eine Erstansage der RE-Partei. Die genaue Stärke des Blattes hängt neben dem Spielverlauf (wieviel Stiche hat die RE-Partei schon?; welche Stärken haben die Spieler der RE-Partei versprochen? etc.) auch sehr stark von der Sitzposition der einzelnen Spieler ab. Betrachten wir zunächst die Erstansage: Eine Ansage hinter dem Hochzeiter sitzend ist mit einem "schwächeren" Blatt möglich als vor dem Hochzeiter sitzend.
Dies ist aus zwei Gründen so:
- Hinter dem Hochzeiter sitzend weiß der Spieler schon, daß der Hochzeiter selbst keine Erstansage getroffen hat. Er kann das Blatt seines Partners daher etwas aufwerten. Vor dem Hochzeiter sitzend hat der Spieler noch keinen direkten Anhaltspunkt über die Stärke
des Blattes des Hochzeiters.
- Hohe Trumpf - hier vor allen Dingen
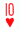 (en) - sind hinter dem Hochzeiter wesentlich wirksamer, da sie den i.d.R. stärkeren Spieler der RE-Partei kontrollieren können.
(en) - sind hinter dem Hochzeiter wesentlich wirksamer, da sie den i.d.R. stärkeren Spieler der RE-Partei kontrollieren können.
Vor dem Hochzeiter sitzend hat der Spieler einen wesentlichen geringeren Einfluß auf den Spielverlauf. Hieraus folgt, daß selbst mit starken Blättern direkt vor dem Hochzeiter sitzend häufig auf eine Ansage verzichtet wird. Man setzt hier häufig das Mittel der Anfrage an den Partner ein, wenn dieser noch hinter dem Hochzeiter sitzt. Eine Anfrage ist auch hier immer gleichzusetzen mit der Frage an den Partner, ob er den Stich machen kann. Einige Beispiele die die Abhängigkeit der Sitzposition näher beleuchten: (...)
Solo
(...)
Assolo
Das Assolo ist das schwächste Solo in der obigen Kette, d.h. ein Assolo wird von einem Spieler auch relativ häufig gewählt, wenn der Erwartungswert für das Solo negativ ist. Der Solospieler muß also nicht unbedingt mit einem Gewinn rechnen, d.h. das Erreichen von 90 Augen ohne eine KONTRA-Ansage kann häufig bereits als Erfolg gewertet werden. Wir unterscheiden zwei Typen von Assoli:
- Standardassolo:
Der Solospieler hat Anspiel und zieht seine Stiche von oben ab.
- Entwicklungsassolo:
Der Solospieler geht freiwillig vom Spiel (z.B. zur Entwicklung einer Farbe) oder die Gegenpartei besitzt Anspiel.
Standardassolo
Der Solospieler besitzt i.d.R. eine lange Farbe (5-7, selten 8 Karten), in der er wahrscheinlich keinen Abgeber besitzt, und As(se) in den Nebenfarben. Ein solches Solo ist bei 9 Stichen immer gewonnen und bei 7 Stichen i.d.R. verloren (lediglich bei einigen Extremverteilungen bestehen Gewinnaussichten). Von Interesse ist der Fall, daß der Solospieler 8 Stiche besitzt. Die folgende Tabelle, in denen die Mindestaugenzahl des Solospielers in Abhängigkeit von der genauen Struktur seines Blattes eingetragen ist, zeigt, daß es hier von enormer Bedeutung ist, daß dem Solospieler nicht unnötig Augen geschenkt werden: (...)
Gegenspiel (As-Signal-Konvention)
Von einem Gegenspiel kann gegen diesen Typ des Solos eigentlich keine Rede sein. Die Gegenspieler können i.d.R. lediglich auf die Standkarten des Solospielers abwerfen. Diese Abwürfe sind allerdings nach Beendigung des Bedienens frei wählbar. Es besteht also die Möglichkeit durch die Reihenfolge der Abwürfe seinen Mitspielern Informationen zukommen zu lassen. Die wichtigste Information für die Gegenspieler ist: Welche Nebenstiche besitzt der Solospieler. Um zu verhinderung, daß dem Solospieler unnötig Volle geschenkt werden hat sich nun das folgende konventionelle System bewährt, welches durch die Reihenfolge der freiwilligen Abwürfe auf die lange Farbe des Solospielers den Mitspielern zeigt, welche Asse die einzelnen Spieler halten. Hieraus ist dann ein Rückschluß auf die Nebenstiche des Solospielers möglich. Diese Information ist zwar auch für den Solospieler zugänglich, allerdings nur in sehr seltenen Fällen von praktischem Nutzen. Wie wichtig eine einwandfreie Konvention für dieses Gegenspielproblem ist zeigt das folgende Beispiel: (...)
Bei der As-Signal-Konvention gelten folgende Regeln für die freiwilligen Abwürfe:
- Es werden möglichst eindeutig so viele Asse wie möglich mit Ausnahme von Doppelassen gezeigt.
- Der Abwurf einer Karte signalisiert: Wahrscheinlich ein As in der Farbe des Abwurfes.
- Ein Farbwechsel bestätigt das Vorhandensein des Asses, der zuvor gelegten Farbe.
- Es wird kein Voller Singleton gestellt, es sei denn der Spieler hält mehr als 4 Volle oder beide Asse sind bei der KONTRA-Partei.
- Asse, die aufgrund von Regel 3 nicht gezeigt werden können (z.B. bei As x oder As 10 x)werden durch ein Hoch-Niedrig-Signal bei Abwurf einer anderen Farbe gezeigt. Ein Hoch-Niedrig-Signal kann dabei durch eine Karte einer anderen Farbe unterbrochen werden.
- Die Signalfolge ist beendet, wenn eine Farbe wiederholt wird, oder wenn nach einem Hoch-
- Niedrig-Signal die Farbe gewechselt wird.
(...)
Ansageverhalten der Gegenspieler
(....)
Entwicklungssolo
Der Einsatz der Hilfsmittel beim Standardsolo war beschränkt, da die KONTRA-Partei über keinen Einfluß auf den Spielverlauf besitzt. Etwas anders sieht die Situation beim Entwicklungssolo aus. Hier bestehen eine Vielzahl von Möglichkeiten für den Einsatz von vorzeitigen Ansagen oder auch Anfragen.
Ansagen und Ansagezeitpunkte
Aufgrund der Argumentation in der Einführung zu diesem Kapitel beschäftigen wir uns nur mit der Interpretation von vorzeitigen Ansagen. Ansagen zum letztmöglichen Zeitpunkt können auch getroffen werden, wenn der Spieler nicht nur aufgrund seines eigenen Blattes der Meinung ist, daß der Solospieler kein gewinnbares Solo besitzt. Vorzeitige Ansagen zeigen immer, daß der Spieler mit einer hohen Wahrscheinlichkeit glaubt das Solo schlagen zu können bzw. eine adäquate Erhöhung der Gewinnaussichten durch die Ansage vorliegt. Dabei wird wieder zwischen einer Ansage als Kommentar zu einer Karte oder vor dem Anspiel unterschieden. Im folgenden sind in Abhängigkeit von der jeweiligen Situation typische Interpretationen für eine vorzeitige Ansage aufgezeigt: (...)
Buben-/Damen-Solo
Das Bubensolo ist nach dem Assolo das nächst schwächere Solo, gefolgt vom Damensolo, d.h.
beim Bubensolo ist die Wahrscheinlichkeit, daß es auch mit einem wissentlichen negativen Erwartungswert
gespielt wird zwar geringer als beim Assolo allerdings höher als beim Damensolo.
Damensolo mit negativem Erwartungswert werden schon recht selten gespielt, da der Spieler
meistens im Besitz einer ![]() ist und damit der Partei angehört, die circa 70% der Normalspiele
gewinnt. Hierdurch folgt, daß Ansagen (vor allen Dingen bei einem Damensolo ) nur dann getroffen
werden sollten, wenn der Gegenspieler aufgrund der Kartenverteilung erkennen kann,
daß der Solospieler wahrscheinlich 1 bis 2 eingeplante Stiche nicht erhält. Dies ist i.d.R bei einer
unerwarteten Trumpfverteilung oder Abstechen von As(sen) des Solospielers der Fall. Hierbei
können die bekannten Hilfsmittel des Essener Systems (vorzeitige, häufig konventionelle Ansagen
bzw. Anfragen) angewendet werden:
ist und damit der Partei angehört, die circa 70% der Normalspiele
gewinnt. Hierdurch folgt, daß Ansagen (vor allen Dingen bei einem Damensolo ) nur dann getroffen
werden sollten, wenn der Gegenspieler aufgrund der Kartenverteilung erkennen kann,
daß der Solospieler wahrscheinlich 1 bis 2 eingeplante Stiche nicht erhält. Dies ist i.d.R bei einer
unerwarteten Trumpfverteilung oder Abstechen von As(sen) des Solospielers der Fall. Hierbei
können die bekannten Hilfsmittel des Essener Systems (vorzeitige, häufig konventionelle Ansagen
bzw. Anfragen) angewendet werden:
Ansagezeitpunkte
Eine vorzeitige Ansage wird aus dem zu vermutenden positiven Erwartungswert nur dann freiwillig getroffen, wenn die damit gezeigte Information für die eigene Partei wichtiger als für den Solospieler ist bzw. der Solospieler die gezeigte Information schon kennt: Die genaue Interpretation einer vorzeitigen Ansage hängt vom Anspiel und dem anspielenden Spieler ab. Betrachten wir zunächst einige typische Anspiele des Solospielers (bei den Beispielen wird jeweils von einem Bubensolo ausgegangen, bei einem Damensolo gelten die Angaben analog):
1) Solospieler spielt zum ersten Stich ![]() an
Eine vorzeitige Ansage ist bei diesem Anspiel ein Zeichen von Stärke, wobei ein starkes Blatt
immer Trumpfstärke bedeutet. Ein Solospieler kann sein Solo gegen 4 Asse bei einem Spieler
trotzdem gewinnen, aber selten gegen 4 Buben. Der genaue Zeitpunkt zeigt die Stärke der
eigenen Trumpf hinsichtlich Anzahl und Höhe. Es gelten folgende Vereinbarungen:
an
Eine vorzeitige Ansage ist bei diesem Anspiel ein Zeichen von Stärke, wobei ein starkes Blatt
immer Trumpfstärke bedeutet. Ein Solospieler kann sein Solo gegen 4 Asse bei einem Spieler
trotzdem gewinnen, aber selten gegen 4 Buben. Der genaue Zeitpunkt zeigt die Stärke der
eigenen Trumpf hinsichtlich Anzahl und Höhe. Es gelten folgende Vereinbarungen:
- Ein KONTRA bei Legen einer fremden Karte (Trumpf) zeigt eine höhere Trumpfzahl (auf einen
angespielten ![]() 5, auf einen gelegten Buben eines Partners 4 etc.) als der Solospieler
unabhängig von der eigenen Höhe der Trumpf.
5, auf einen gelegten Buben eines Partners 4 etc.) als der Solospieler
unabhängig von der eigenen Höhe der Trumpf.
- Ein KONTRA mit Legen der eigenen Karte (Trumpf) zeigt exakt 4 Buben mit Wirkung. Wirkung
bedeutet inklusive Doppel-![]() oder einem
oder einem ![]() .
Hieraus folgt, daß in folgendem Stich
.
Hieraus folgt, daß in folgendem Stich ![]()
![]()
![]()
![]() +KO(3) Spieler 3 genau
+KO(3) Spieler 3 genau ![]()
![]()
![]()
![]() besitzt! Es sollte jeweils der Bube mit dem höchsten Informationsgehalt gelegt werden: Bei einer
Kombination
besitzt! Es sollte jeweils der Bube mit dem höchsten Informationsgehalt gelegt werden: Bei einer
Kombination ![]()
![]()
![]()
![]() wird daher
wird daher ![]() mit KONTRA gelegt. Eine vorzeitige Ansage ist in
diesen Fällen ungefährlich, da der Solospieler nach dem ersten Stich i.d.R. sowieso die TrumpfSoloverteilung kennt und in dem Fall, daß er trotzdem noch ein gewonnenes Solo besitzt, auf eine
KONTRA-Ansage der Gegenpartei warten wird. Die eigene Partei ist allerdings ohne die Ansage
nicht über die Trumpfverteilung informiert. (...)
mit KONTRA gelegt. Eine vorzeitige Ansage ist in
diesen Fällen ungefährlich, da der Solospieler nach dem ersten Stich i.d.R. sowieso die TrumpfSoloverteilung kennt und in dem Fall, daß er trotzdem noch ein gewonnenes Solo besitzt, auf eine
KONTRA-Ansage der Gegenpartei warten wird. Die eigene Partei ist allerdings ohne die Ansage
nicht über die Trumpfverteilung informiert. (...)
2) Solospieler spielt zum ersten Stich ![]() an.
an.
Ein sofortiges freiwilliges KONTRA zeigt 4-5 Buben mit einem ![]() oder 3 Buben mit
oder 3 Buben mit ![]()
![]() an.
Hier reichen 4 Buben, da die KONTRA-Partei am Spiel ist und somit die Initiative besitzt. Der
Solospieler kann sehr häufig zuerst in Trumpf gekürzt werden. Das Legen einer kleinen Karte
(oder As) eines Partners nach der Ansage ist hier ein starkes direktes Signal für die abgeworfenen
Farbe. Es wäre unsinnig in einen eigenen Stich eine kleine Karte zu legen, d.h. diese Aktion
muß eine Bedeutung haben. Beim Anspiel des
an.
Hier reichen 4 Buben, da die KONTRA-Partei am Spiel ist und somit die Initiative besitzt. Der
Solospieler kann sehr häufig zuerst in Trumpf gekürzt werden. Das Legen einer kleinen Karte
(oder As) eines Partners nach der Ansage ist hier ein starkes direktes Signal für die abgeworfenen
Farbe. Es wäre unsinnig in einen eigenen Stich eine kleine Karte zu legen, d.h. diese Aktion
muß eine Bedeutung haben. Beim Anspiel des ![]() ist es nur wahrscheinlich ein Signal, da alle Spieler sowieso eine kleine Karte irgendeiner Farbe abgeworfen hätten. Ein KONTRA mit Legen
der eigenen Karte zeigt nun 5 Buben ohne
ist es nur wahrscheinlich ein Signal, da alle Spieler sowieso eine kleine Karte irgendeiner Farbe abgeworfen hätten. Ein KONTRA mit Legen
der eigenen Karte zeigt nun 5 Buben ohne ![]() , da mit 4 Buben ohne
, da mit 4 Buben ohne ![]() systemgemäß kein
vorzeitiges KONTRA gerechtfertigt ist (Ausnahme: hinter dem Spieler mit den 4 Buben wird ein
weitere Bube der eigenen Partei gelegt, dann KONTRA) und da mit 5 Buben diesmal kein vorzeitiges
KONTRA erfolgen konnte (kollidiert mit der ersten Variante; die Partner würden eventuell
Volle schmieren). Die Partner sollten nach Möglichkeit wieder gute Farben signalisieren.
Bisher haben wir den Solospieler immer einen Buben zum ersten Stich anspielen lassen. Hierdurch
konnte immer eindeutig eine vorzeitige Ansage getätigt werden. Es kann nun allerdings
passieren, daß der Solospieler zunächst ein As spielt oder erst eine Farbe stechen mußte bzw.
angespielt wurde. Wir erinnern daran, daß im zweiten Stich ebenfalls eine vorzeitige Ansage mit
Legen der eigenen Karte erfolgen kann, indem der Spieler nach Legen der Karte seines Vorgängers
die Ansage deutlich vor Legen seiner eigenen Karte trifft.
systemgemäß kein
vorzeitiges KONTRA gerechtfertigt ist (Ausnahme: hinter dem Spieler mit den 4 Buben wird ein
weitere Bube der eigenen Partei gelegt, dann KONTRA) und da mit 5 Buben diesmal kein vorzeitiges
KONTRA erfolgen konnte (kollidiert mit der ersten Variante; die Partner würden eventuell
Volle schmieren). Die Partner sollten nach Möglichkeit wieder gute Farben signalisieren.
Bisher haben wir den Solospieler immer einen Buben zum ersten Stich anspielen lassen. Hierdurch
konnte immer eindeutig eine vorzeitige Ansage getätigt werden. Es kann nun allerdings
passieren, daß der Solospieler zunächst ein As spielt oder erst eine Farbe stechen mußte bzw.
angespielt wurde. Wir erinnern daran, daß im zweiten Stich ebenfalls eine vorzeitige Ansage mit
Legen der eigenen Karte erfolgen kann, indem der Spieler nach Legen der Karte seines Vorgängers
die Ansage deutlich vor Legen seiner eigenen Karte trifft.
3) Solospieler spielt As an.
Ein vorzeitiges KONTRA als Kommentar zur Karte zeigt, daß der Spieler diese Farbe stechen kann. Er sollte dazu an Position 3 oder 4 sitzen. Die Idee ist, daß die Partner schmieren können. Die Ansage sollte allerdings freiwillig nur mit Zusatzwerten in Form von Assen und/oder Stellungen (z. B.: As 10 x) erfolgen. Ebenso fordert ein Spieler einen Partner, der einen Stich macht (sei es er wurde angespielt oder er spielt ein As, welches i.d.R von einer langen Farbe angegriffen wird) durch eine vorzeitige Ansage dazu auf die Farbe nachzuspielen. Die Ansage erfolgt i.d.R. nachdem der Solospieler zum Stich eine Karte zugegeben hat.
Anfragen
Alle Anfragen haben zumeist die gleiche Bedeutung wie in den anderen Kapiteln. Der Spieler fragt seinen Partner, ob er den Stich macht bzw. ob er eine bestimmte Karte besitzt oder bestimmte Karten nicht besitzt. Alle Anfragen sind zumindest stark einladend, häufig sogar forcierend. Die Bedeutung einer Anfrage hängt von der jeweiligen Situation ab. Zwei typische Fälle, die bei den Buben/Damen-Soli häufiger vorkommen, sind:
1) Der Solospieler spielt ![]() auf
Ein Warten eines Spielers vor Legen seiner eigenen Karte zeigt den Besitz eines
auf
Ein Warten eines Spielers vor Legen seiner eigenen Karte zeigt den Besitz eines ![]() in Verbindung
mit einem oder zwei weiteren Buben. Die Idee dieser Anfrage ist den Zusammenfall beider
in Verbindung
mit einem oder zwei weiteren Buben. Die Idee dieser Anfrage ist den Zusammenfall beider
![]() in einem Stich zu verhindern. Der Partner mit dem anderen
in einem Stich zu verhindern. Der Partner mit dem anderen ![]() sollte nun KONTRA ansagen,
damit der fragende Spieler klein bleiben kann. Bei vorgeführten Soli kann auch gelegentlich ohne
Trumpf gewartet werden, allerdings sollte dann durch den Abwurf bei positiver Antwort eine gute
Farbe (direkt) angezeigt werden.
sollte nun KONTRA ansagen,
damit der fragende Spieler klein bleiben kann. Bei vorgeführten Soli kann auch gelegentlich ohne
Trumpf gewartet werden, allerdings sollte dann durch den Abwurf bei positiver Antwort eine gute
Farbe (direkt) angezeigt werden.
2) Der Solospieler spielt ein As Das Warten zeigt hier ein gutes Blatt (Trumpf und Asse bzw. Stellungen). Der Spieler, der diese Farbe stechen kann, sollte nun unabhängig von der Stärke seines Blattes KONTRA ansagen. Genauso kann ein Spieler, der einen Fehlstich gemacht hat seine Partner fragen, ob er die Farbe fortsetzten soll. Prinzipiell liegt bei diesem Anspiel die gleiche Situation wie bei gleichem Anspiel bei einer vorzeitigen Ansage vor. Lediglich die Verantwortung wird getauscht, was bedeutet: Bei einer Anfrage sind die benötigten Zusatzwerte beim fragenden Spieler und bei einer freiwilligen Ansage beim ansagenden Spieler.
Dies waren die typischsten Situationen einer vorzeitigen Ansage oder Anfrage bei einem Buben/ Damen-Solo. Die Idee aller geschilderten Varianten ist eine wertvolle Information zu übermitteln, um die Gewinnaussichten (genauer: die Punktausbeute) zu steigern.
Farbensolo
Farbensoli werden freiwillig nur dann gespielt, wenn der Spieler glaubt mit dem Solo eine höhere Punktausbeute zu erzielen. Der Erwartungswert eines solchen Solos ist i.d.R. positiv, da er nebenbei auf ein gutes Normalspiel verzichtet hat. Bei dem Ansageverhalten gegen ein solches Solo, sofern es nicht eine Vorführung ist oder ein Spieler zuvor einen Vorbehalt angemeldet hat, ist größte Vorsicht geboten. Eine Ansage erscheint nur sinnvoll, wenn der Solospieler mit einer ungewöhnlichen Fehlverteilung konfrontiert werden kann oder ein Spieler ein außergewöhnlich starkes Gegenblatt hält. Vorzeitige Ansagen erfolgen i.d.R. nur auf angespielte Asse des Solospielers, wenn ein Spieler dies an Position 3 oder 4 stechen kann. Ein Warten fragt i.d.R. einen weiter hintensitzenden Spieler, ob er den Stich machen kann. Sie sollten allerdings i.d.R. nur mit starken Gegenblättern gestellt werden. An dieser Stelle seien daher nur noch 2 besondere Situationen besprochen:
1) Der Solospieler spielt ein As an und Spieler 2 bedient sehr schnell mit einer kleinen Karte.
Bedeutung: Der Spieler besitzt ein Singleton in der Farbe. Dies erscheint deswegen logisch, da er keinem weiter hintensitzenden Spieler die Gelegenheit einer vorzeitigen Ansage läßt.
2) Spieler 2 legt auf einen kleinen angespielten Trumpf eine unnötig höhere Karte
(auf ![]() beispielsweise
beispielsweise ![]() )
)
Bedeutung: Der Spieler will ans Spiel. Dies ist unnatürlich, da es i.d.R. besser ist, wenn der rechts vom Solospieler sitzende Spieler den Stich macht, damit der Solospieler im nächsten Stich an Position 2 sitzt. Daraus folgt: Spieler 2 kann nicht anders oder er will eine wichtige Information mitteilen. Er kann ein Singleton nachspielen und zeigt somit an, welche Fehlfarbe für den Solospieler unangenehm ist. Die Unterscheidung der beiden Fälle folgt im nächsten Trumpfstich: Legt der Spieler 2 nun eine kleinere Karte als zum vorherigen Stich, so hat er ein Singleton angespielt.
Damit wollen wir nun das Thema Solo abschließen. Wir wollten zeigen, daß (mit Einschränkungen) die Hilfsmittel des Essener Systems auch beim Solo angewendet werden können. Dabei bleiben viele der Grundbedeutungen im Vergleich zu den vorherigen Kapiteln gleich. Eine Optimierung (Ausreizen) des Spieles ist i.d.R. nicht möglich, da wir von einem freiwilligen Solo ausgehen und dem Solospieler schon zugestehen wollen die Stärke seines Solos einschätzen zu können. Wollte man hierzu noch etwas schreiben, so müßte ein ausführlicheres Kapitel über vorgeführte Soli angehängt werden. Wir haben an den meisten Stellen von genauen Beispielblättern für die Anwendung eines bestimmten Hilfsmittels abgesehen, da die benötigte Stärke für die Anwendung dieser Hilfsmittel sehr stark von der vermuteten Stärke des Solos abhängt.
Ausflug in die Wahrscheinlichkeitsrechnung
Einleitung
Ein Doppelkopfspieler muß schon nach dem Aufnehmen der Karten eine Entscheidung treffen. Er fragt sich, ob er mit seinem Blatt ein Solo spielen will oder ein Normalspiel vorzieht. Während des Spieles muß er entscheiden, welche Ansagen er treffen will. Je öfter er sich richtig entscheidet, desto mehr Punkte kann er auf seinem Konto verbuchen. Wenn man im Normalspiel tiefe Ansagen treffen will, sollte man wissen, mit welchen Trumpfverteilungen man rechnen muß. Will man einen As-Soli spielen, so sollte man wissen, wie zuversichtlich man sein kann, daß die lange Farbe durchzieht (Standard-As-Soli) und wenn man bei einem Buben-Solo vermutlich mehrfach vom Stich gehen muß, um eine Farbe zu entwickeln, so sollte man wissen, ob man damit rechnen muß, daß man wegen eines schlechten Sitzes der Buben gar nicht dazu kommt, die Farbe zu entwickeln.
Sind die kritischen Karten in diesen Beispielen günstig verteilt, so gewinnt man i.d.R. das Spiel, sonst verliert man.
Um die richtigen Entscheidungen treffen zu können, muß man also eine Vorstellung darüber haben, welche Verteilungen möglich sind und wie häufig diese jeweils vorkommen. Die Wahrscheinlichkeitsrechnung bietet nun die Möglichkeit die Häufigkeiten der verschiedenen kritischen Verteilungen vorauszusagen. Wenn man seine Entscheidung von diesen Verteilungswahrscheinlichkeiten abhängig macht, wird man auf Dauer mehr Punkte sammeln, als wenn man diese Entscheidungen aus dem Bauch heraus trifft, da die Intuition täuschen kann. Das Spiel mit der Wahrscheinlichkeit verspricht allerdings nur Gewinne auf lange Sicht. Im Einzelfall können bestimmte Karten durchaus völlig falsch sitzen, auch wenn dies extrem unwahrscheinlich ist.
Als Maß für den Wert eines Blattes dient der Erwartungswert, des Blattes. Dies ist die durchschnittliche Punktzahl, die man mit seinem Blatt in Abhängigkeit von den verschiedenen Verteilungen erzielt. Das Ziel ist es, diejenige Spielweise zu wählen, bei der der Erwartungswert möglichst groß ist. Bei Normalspielen ist der Erwartungswert häufig schwer zu berechnen, da er dort oft von einer Vielzahl von Faktoren abhängt. Beim Solo ist die Berechnung meistens erheblich leichter durchzuführen, da hier nur ein oder zwei Faktoren wichtig sind. Daher wird sich dieses Kapitel auch zu einem großen Teil mit den Fragestellungen aus dem Solo beschäftigen.
Grundbegriffe der Wahrscheinlichkeitsrechnung
Die Wahrscheinlichkeitsrechnung befaßt sich mit den Vorgängen, deren Ausgang nicht vorhersagbar ist. Dies kann daran liegen, daß man gewisse Bedingungen, unter denen ein solcher Vorgang stattfindet, nicht kennt oder daran, daß der Vorgang selbst nicht vollständig durchschaut wird. Wirft man beispielsweise eine Münze in die Luft, so kann nicht vorhergesagt werden, ob Kopf oder Zahl nach oben zeigen wird. Um dies vorauszuberechnen müßte man umfangreiche Daten über den Münzwurf zusammentragen (Stärke des Wurfes, Anfangsrotation der Münze, Materialverteilung in der Münze und damit das Rotationsverhalten der Münze, Luftdruck etc.).
Wiederholt man den Münzwurf sehr oft, wird man feststellen, daß jede Seite in etwa der Hälfte der Fälle nach oben zeigt (wenn es sich nicht gerade um eine deformierte Münze handelt). Die einander ausschließenden möglichen Ausgänge eines Versuches heißen Elementarereignisse. Der Münzwurf hat zwei Elementarereignisse: 1) "Kopf weist nach oben" und 2) "Zahl weist nach oben". Beim Werfen eines Würfels gibt es sechs einander ausschließende Elementarereignisse.
Jeder mögliche Ausgang eines Versuches wird Ereignis genannt. Ein Ereignis kann aus mehreren Elementarereignissen zusammengesetzt sein. So ist das Ereignis "man würfelt eine gerade Zahl" aus den Elementarereignissen "man würfelt eine zwei", "man würfelt eine vier" und "man würfelt eine sechs" zusammengesetzt. Zwei Ereignisse heißen unvereinbar, wenn sie nicht gleichzeitig eintreten können. Man kann z.B. mit einem Würfel nicht gleichzeitig eine vier und eine ungerade Zahl würfeln. Zwei Ereignisse heißen unabhängig, wenn das Eintreten des einen Ereignisses keinen Einfluß auf das Eintreten des anderen Ereignisses hat. Würfelt man zweimal hintereinander, so beeinflußt der erste Wurf sicherlich nicht den Ausgang des zweiten Wurfes.
Kommen wir nun zur klassischen Definition der Wahrscheinlichkeit (dies setzt voraus, daß es endlich viele Elementarereignisse gibt, die alle gleichmöglich sind). Die Wahrscheinlichkeit, daß ein Ereignis A eintritt wird definiert als:
p(A) =Anzahl aller möglichen Elementarereignisse / Anzahl der für A günstigen Elementarereignisse
Die Wahrscheinlichkeit eine drei zu würfeln ist also 1/6. Die Wahrscheinlichkeit eine gerade Zahl zu würfeln ist 3/6 = 1/2. Das sichere Ereignis "man würfelt eine Zahl von eins bis sechs" hat die Wahrscheinlichkeit 6/6 = 1. Das unmögliche Ereignis "man würfelt eine sieben" hat die Wahrscheinlichkeit 0/6 = 0. Wahrscheinlichkeiten werden also durch Zahlen zwischen 0 und 1 repräsentiert. Häufig werden sie jedoch als Prozentzahlen dargestellt, indem sie einfach mit 100 multipliziert (und mit einem Prozentzeichen versehen) werden. Das sichere Ereignis hat dann die Wahrscheinlichkeit von 100% und das unmögliche Ereignis hat die Wahrscheinlichkeit 0%.
Man steht häufig vor der Frage, wie wahrscheinlich ist es, daß entweder ein Ereignis A oder ein Ereignis B eintritt. Sind diese Ereignisse A und B unvereinbar, so kann die gesuchte Wahrscheinlichkeit leicht berechnet werden, denn es gilt:
Man steht häufig vor der Frage, wie wahrscheinlich ist es, daß entweder ein Ereignis A oder ein Ereignis B eintritt. Sind diese Ereignisse A und B unvereinbar, so kann die gesuchte Wahrscheinlichkeit leicht berechnet werden, denn es gilt:
Regel 1: Die Wahrscheinlichkeit, daß von zwei unvereinbaren Ereignissen A und B wenigstens eines eintritt, ist die Summe der beiden Einzelwahrscheinlichkeiten.
- p(A oder B) = p(A) + p(B)
Dies gilt analog auch für mehr als zwei unvereinbare Ereignisse. Ebenso häufig möchte man wissen, wie wahrscheinlich es ist, daß sowohl Ereignis A als auch Ereignis B eintritt. Sind A und B unabhängig voneinander, so gilt die
Regel 2: Die Wahrscheinlichkeit, daß die voneinander unabhängigen Ereignisse A und B beide eintreten, ist das Produkt der Einzelwahrscheinlichkeiten.
- p(A und B) = p(A) × p(B)
Auch dies kann man für mehrere Ereignisse verallgemeinern. Leider ist es häufig so, daß die Ereignisse nicht unabhängig sind. Ganz allgemein gilt die
Regel 3: Die Wahrscheinlichkeit, daß die Ereignisse A und B beide eintreten ist das Produkt der Wahrscheinlichkeiten von A mit der Wahrscheinlichkeit von B unter der Voraussetzung, daß A eingetreten ist.
- p(A und B) = p(A) × p(B, vorausgesetzt A ist eingetreten)
Ein Beispiel:
A sei das Ereignis "man würfelt eine Zahl kleiner als vier" und B das Ereignis "man würfelt eine ungerade Zahl" Hier kann man das Ergebnis auch ohne große Rechnung angeben, da offensichtlich nur die Elementarereignisse "man würfelt eine 1" und "man würfelt eine drei" günstig sind. Also ist die Wahrscheinlichkeit 2/6 = 1/3. Versuchen wir noch die Rechnung nach der Regel 3. Die Wahrscheinlichkeit für das Würfeln einer Zahl kleiner vier ist 3/6 = 1/2. Die Wahrscheinlichkeit eine ungerade Zahl zu würfeln unter Voraussetzung Ereignis A ist eingetreten offensichtlich 2/3. Dann ergibt sich nach Regel 3 mit p(A und B) = 1 2 × 2 3 = 1 3 das erwartete Ergebnis. Die Regel 2 ist ein Sonderfall der Regel 3 für unabhängige Ereignisse.
Bei den meisten Berechnungen reicht es aus so zu tun, als ob die Ereignisse unabhängig wären, da der entstehende Fehler ziemlich klein ist, während der gesparte Arbeitsaufwand meist recht groß ist. Spielt man z.B. als Hochzeiter zum ersten Stich sein blankes ![]() und es fallen
und es fallen ![]()
![]()
![]() , so weiß man, daß die restlichen
, so weiß man, daß die restlichen ![]() 4-0-0 verteilt sind.
4-0-0 verteilt sind.
Berechnet man nun, wie wahrscheinlich es ist, daß jeder Spieler mindestens ein ![]() hält, wenn man selbst
hält, wenn man selbst ![]()
![]()
![]() hat, so beträgt sie 64,2%. Wäre das
hat, so beträgt sie 64,2%. Wäre das ![]() nichtssagend gelaufen, wären es 67,3%. Der Rechenaufwand für die erste Zahl ist erheblich größer (wer will kann es ja nachprüfen), doch der Fehler ist nicht besonders groß, obwohl schon eine ziemlich extreme Verteilung vorliegt. Braucht man also keine genauen, sondern reichen ungefähre Zahlen, lohnt sich der Aufwand nicht.
nichtssagend gelaufen, wären es 67,3%. Der Rechenaufwand für die erste Zahl ist erheblich größer (wer will kann es ja nachprüfen), doch der Fehler ist nicht besonders groß, obwohl schon eine ziemlich extreme Verteilung vorliegt. Braucht man also keine genauen, sondern reichen ungefähre Zahlen, lohnt sich der Aufwand nicht.
Will man schließlich wissen, wann von zwei Ereignissen, die miteinander vereinbar sind, wenigstens eines eintritt, muß man die Regel 1 abändern. Es gilt allgemein die
Regel 4: Die Wahrscheinlichkeit, daß von zwei Ereignissen A und B wenigstens eines eintritt, ist die Summe der beiden Einzelwahrscheinlichkeiten verringert um die Wahrscheinlichkeit, daß beide Ereignisse eintreten.
- p(A oder B) = p(A) + p(B) - p(A und B)
Die Regel 1 wird damit zum Sonderfall der Regel 4, wenn p(A und B) = 0 ist, was genau dann der Fall ist, wenn A und B unvereinbar sind.
Die Hypergeometrische Verteilung
(...)
Tab. A1:Verteilungswahrscheinlichkeiten
Die Wahrscheinlichkeiten für n = 11 (also in Kenntnis des ersten Stiches) gelten streng genommen nur, wenn im ersten Stich alle Spieler bedient haben mit den interessanten Karten und die interessanten Karten alle keinen besonderen Informationsgehalt bezüglich der Verteilung der restlichen Karten besitzen. Für den Fall, daß eine besondere Karte (woraus folgt: Der Spieler besitzt keine weitere der kritischen Karten) gefallen ist oder ein Spieler nicht bedient hat, kann die Tabelle A2 herangezogen werden.
Tab. A2:Verteilungswahrscheinlichkeiten
Diese beiden Tabellen (auf Formel 2 basierend) sind die Grundlage für alle weiteren Berechnungen. Mit ihrer Hilfe und den Regeln 1-3 der Wahrscheinlichkeitsrechnung ist es möglich eine Vielzahl für den Doppelkopfspieler relevanten Wahrscheinlichkeiten näherungsweise zu berechnen. Strenggenommen darf man nicht mit den Verteilungswahrscheinlichkeiten aus Tabelle A1 arbeiten,
da schon durch die Vorbehaltsabfrage Informationen über den Spielverlauf gegeben werden, die die Wahrscheinlichkeiten verändern. Genauer müßten mit Formel 3 die Wahrscheinlichkeiten neu berechnet werden, wobei allein schon zwischen RE-Spieler und KONTRA-Spieler
unterschieden werden müßte (durch den Besitz, bzw. Nichtbesitz von §D hat der Spieler entweder schon eine bestimmte Karte bzw. ihm stehen bei der Austeilung definitiv nur 46 Karten zur Verfügung). Doch hier gilt , daß in den meisten Fällen die Abweichung klein ist, während der zusätzliche Aufwand groß ist. Die Verteilungswahrscheinlichkeiten aus Tabelle A1 sind für Spieler mit mindestens einer ![]() und für Solospieler links vom Geber, die ihr Solo taufen bevor die anderen Spieler einen Vorbehalt melden konnten, korrekt, da hier die Vorbehaltsabfrage keinerlei Informationen enthält.
und für Solospieler links vom Geber, die ihr Solo taufen bevor die anderen Spieler einen Vorbehalt melden konnten, korrekt, da hier die Vorbehaltsabfrage keinerlei Informationen enthält.
Berechnung nützlicher Wahrscheinlichkeiten
Es folgen nun einige Beispiele für die Anwendung der Tabellen A1 und A2 zur Berechnung von Wahrscheinlichkeiten. Bei der Berechnung wird - wenn nicht ausdrücklich etwas anderen angegeben wird - immer von der Situation unmittelbar vor Spielbeginn ausgegangen. Einige wichtige Wahrscheinlichkeiten für den täglichen Gebrauch sind dann in den Tabellen A3 bis A7 dargestellt.
Beispiel 1
Spieler hält 9 Trumpf und ![]()
![]()
![]() als Fehlkarten
als Fehlkarten
Wie wahrscheinlich ist es nun , daß
- kein Mitspieler gleich viele Trumpf als er selbst hält,
- das
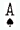 läuft und
läuft und - er beide
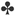 -Runden alleine sticht.
-Runden alleine sticht.
Beispiel 1 zu 1.
Es fehlen 26 - 9 = 17 Trumpf = interessante Karten.
Die günstigen Verteilungen sind:
| Verteilungen | Wahrscheinlichkeiten |
|---|---|
| 6-6-5 | 23,59% |
| 7-5-5 | 17,34% |
| 7-6-4 | 25,28% |
| 7-7-3 | 4,82% |
| 8-5-4 | 13,54% |
| 8-6-3 | 7,02% |
| 8-7-2 | 1,81% |
| 8-8-1 | 0,10% |
| Summe: | 93,50% |
(siehe Tab. A1 für M = 17).
In ungefähr 9 von 10 Fällen besitzt ein Spieler mit 9 Trumpf die absolute Trumpfüberlegenheit. Nehmen wir nun zusätzlich den Fall an, daß zum ersten Stich Trumpf angespielt wird und alle Spieler bedienen, so kann die Wahrscheinlichkeit neu berechnet werden:
Es fehlen nun 26 - 9 - 3 = 14
| Verteilungen | Wahrscheinlichkeiten |
|---|---|
| 5-5-4 | 23,59% |
| 6-4-4 | 18,43% |
| 6-5-3, | 25,81% |
| 6-6-2 | 4,30% |
| 7-4-3 | 13,17% |
| 7-5-2 | 6,14% |
| 7-6-1 | 1,23% |
| 7-7-0 | 0,04% |
| Summe: | 94,93% |
(siehe Tab. A1 für M = 14 und n = 11).
Beispiel 1 zu 2.
Es fehlen bei ![]()
![]() genau 6 interessante Karten. Die günstigen Verteilungen sind alle diejenigen, in denen keiner der übrigen drei Spieler eine Chicane besitzt.
genau 6 interessante Karten. Die günstigen Verteilungen sind alle diejenigen, in denen keiner der übrigen drei Spieler eine Chicane besitzt.
Dies sind:
| Verteilungen | Wahrscheinlichkeiten |
|---|---|
| 2-2-2 | 14,76% |
| 3-2-1 | 53,67% |
| 4-1-1, | 10,98 |
| Summe: | 79,41% |
Bei einer Ansage kommt noch die Fälle hinzu, daß nur der Partner Chicane in der Farbe ist. Der Einfachheit halber nehmen wir an, daß von den Verteilungen, bei denen genau ein Spieler Chicane ist, ein Drittel günstig ist. In Wirklichkeit ist der Anteil für Re-Spieler etwas größer als für einen KONTRA-Spieler.
Wir berücksichtigen noch die Verteilungen:
| Verteilungen | Wahrscheinlichkeiten |
|---|---|
| 5-1-0 | 2,93% |
| 4-2-0 | 10,06% |
| 3-3-0, | 7,45% |
| Günsteige | 79,41% |
| Summe: | 86,22% |
Weitere Angaben zu diesem Thema siehe Tab. A3.
Beispiel 1 zu 3.
Es fehlen insgesamt 8 interessante Karten.
| Verteilungen | Wahrscheinlichkeiten |
|---|---|
| 3-3-2 | 31,67% |
| 4-2-2 | 21,38% |
| Summe: | 53,05% |
Bei einer Ansage erhöht sich Wahrscheinlichkeit analog wie bei dem vorherigen Beispiel, da nun ursprünglich ungünstige Verteilungen teilweise miteinbezogen werden können.
Weitere Werte (mit Ansage d.h. Partner kann mitstechen, Spieler hält keine Chicane sondern Singleton, ![]() -Stechen) befinden sich in Tab. A4.
-Stechen) befinden sich in Tab. A4.
(...) weitere Beispiel fehlen
Tab. A3: Laufwahrscheinlichkeit von Assen im Normalspiel
| fehlende Karten in der kritischen Farbe | 7 | 6 | 5 | 4 | 3 |
|---|---|---|---|---|---|
| Laufwahrscheinlichkeit ohne Ansage | 87,6% | 79,4% | 66,8% | 48,4% | 24,2% |
| Laufwahrscheinlichkeit mit Ansage | 91,7% | 86,2% | 77,7% | 64,8% | 46,4% |
Tab. A4: Wahrscheinlichkeit eine Fehlfarbe allein zu stechen im Normalspiel
| . | zweimaliges Stechen bei Chicane | einmaliges Stechen bei Singleton | ||
| |
|
|
| |
| Laufwahrscheinlichkeit ohne Ansage | 53,1% | 14,8% | 34,4% | |
| Laufwahrscheinlichkeit mit Ansage | 68,2% | 38,5% | 54,7% | 21,6% |
Tab. A5: Wahrscheinlichkeit ein blankes As zu fangen
| fehlende Karten in der kritischen Farbe | 6 | 5 | 4 | 3 | 2 |
|---|---|---|---|---|---|
| Wahrscheinlichkeit, daß As zu fangen | 13,1% | 20,3% | 30,9% | 46,4% | 68,6% |
Tab. A6: Wahrscheinlichkeit alle Buben/Damen beim Buben/Damen-Solo zu fangen
x = beliebige(r) andere(r) rote(r) (![]() /
/![]() )eigen(r) Bube/Dame
)eigen(r) Bube/Dame
Tab. A7: Wahrscheinlichkeit keinen Verlierer mit doppel AS zu besitzen
Wahrscheinlichkeit mit einer langen Farbe mit As As x (=K) an der Spitze keinen Verlierer zu besitzen
| Struktur der Farbe | n = 12 | Struktur der Farbe | n = 12 |
|---|---|---|---|
| As, As, x, x, x, x | 14,8% | As, As, K, x, x | 9,8% |
| As, As, x, x, x, x, x | 41,6% | As, As, K, x, x, x | 25,5% |
| As, As, x, x, x, x, x, x | 70,6% | As, As, K, x, x, x, x | 46,4% |
| As, As, x, x, x, x, x, x, x | 90,8% | As, As, K, x, x, x, x, x | 70,6% |
x = beliebige andere eigene Karte in der Farbe


